题目内容
18.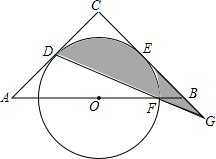 如图,已知△ABC,AC=BC=6,∠C=90°,O是AB的中点,⊙O与AC相切于点D,与BC相切于点E.⊙O交OB于F,连接DF并延长交CB的延长线于G.
如图,已知△ABC,AC=BC=6,∠C=90°,O是AB的中点,⊙O与AC相切于点D,与BC相切于点E.⊙O交OB于F,连接DF并延长交CB的延长线于G.(1)求证:∠BFG=∠G;
(2)求EG的长;
(3)求由DG,GE和$\widehat{ED}$所围成图形的面积(阴影面积).
分析 (1)连接OD.根据切线的性质得到OD⊥AC,则OD∥BC;可得∠ODF=∠G,再结合对顶角相等和等边对等角得到∠BFG=∠BGF.
(2)首先连接OE,由切线的性质,可得四边形ODCE为正方形,则可求得BE与BG的长,继而求得答案;
(3)由阴影部分的面积=直角三角形CDG的面积-(正方形的面积-扇形ODE的面积).根据等腰直角三角形的性质可求出有关边AB、OD的长,以及圆心角∠DOE的度数.进而可根据扇形的面积和直角三角形的面积求得阴影部分的面积.
解答 解:(1)连接OD,
∵OD=OF,
∴∠ODF=∠OFD;
∵⊙O与AC相切于点D,
∴OD⊥AC;
又∵∠C=90°,即GC⊥AC,
∴OD∥GC,
∴∠G=∠ODF;
又∵∠BFG=∠OFD,
∴∠BFG=∠G.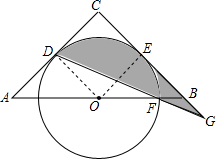 (2)连接OE,
(2)连接OE,
∵⊙O与AC相切于点D、与BC相切于点E,
∴DC=CE,OD⊥AC,OE⊥BC,
∵∠C=90°,
∴四边形ODCE为正方形,
∵AO=BO=$\frac{1}{2}$AB=$\frac{1}{2}$$\sqrt{A{C}^{2}+B{C}^{2}}$=3$\sqrt{2}$,
∴OD=BE=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3,
∵∠BFG=∠BGF,
∴BG=BF=OB-OF=3$\sqrt{2}$-3;
∴EG=BE+BG=3$\sqrt{2}$;
(3)∵CG=CB+BG=3$\sqrt{2}$+3;
∴S阴影=S△DCG-(S正方形ODCE-S扇形ODE)
=$\frac{1}{2}$×3×(3+3$\sqrt{2}$)-(32-$\frac{1}{4}$π×32)
=$\frac{9}{4}$π-$\frac{9}{2}$+$\frac{9}{2}$$\sqrt{2}$.
点评 此题综合考查了切线的性质、平行线的性质、等腰直角三角形的性质及扇形的面积计算方法.注意准确作出辅助线是解此题的关键.

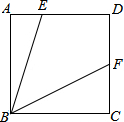 如图,已知正方形ABCD中,E在AD边上,F在CD边上,且∠EBF=45°,若AE=2,CF=3,则AB长( )
如图,已知正方形ABCD中,E在AD边上,F在CD边上,且∠EBF=45°,若AE=2,CF=3,则AB长( )| A. | 5.5 | B. | 6 | C. | 6.5 | D. | 7 |
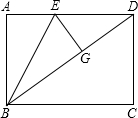 如图,矩形ABCD,AB=3,BC=4,点E是AD上一点,连接BE,将△ABE沿BE折叠,点A恰好落在BD上的点G处,则AE的长为( )
如图,矩形ABCD,AB=3,BC=4,点E是AD上一点,连接BE,将△ABE沿BE折叠,点A恰好落在BD上的点G处,则AE的长为( )| A. | 2 | B. | $\frac{5}{2}$ | C. | $\frac{3}{2}$ | D. | 3 |

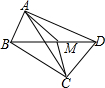 如图,在四边形ABCD中,∠BAD=∠BCD=90°,M是BD的中点,连接AM、CM,那么△MAC是等腰三角形吗?请说明理由.
如图,在四边形ABCD中,∠BAD=∠BCD=90°,M是BD的中点,连接AM、CM,那么△MAC是等腰三角形吗?请说明理由.