题目内容
18.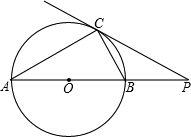 已知:如图,点P在⊙O外,PC是⊙O的切线,C为切点,直线PO与⊙O相交于点A、B.
已知:如图,点P在⊙O外,PC是⊙O的切线,C为切点,直线PO与⊙O相交于点A、B.(1)试探求∠BCP与∠P的数量关系;
(2)若∠A=30°,则PB与PA有什么数量关系?
分析 (1)由PC为圆O的切线,利用弦切角等于夹弧所对的圆周角得到∠BCP=∠A,再由三角形内角和定理及圆周角定理即可确定出两角的关系;
(2)由∠A的度数求出∠BCP的度数,进而确定出∠P的度数,再由PB=BC,AB=2BC,等量代换确定出PB与PA的关系即可.
解答 解:(1)∵点P在⊙O外,PC是⊙O的切线,C为切点,直线PO与⊙O相交于点A、B,
∴∠BCP=∠A,
∵∠A+∠P+∠ACB+∠BCP=180°,AB是⊙O的直径,
∴∠ACB=90°,2∠BCP=180°-∠P,
∴∠BCP=$\frac{1}{2}$(90°-∠P);
(2)若∠A=30°,则∠BCP=∠A=30°,
∴∠P=30°,
∴PB=BC,BC=$\frac{1}{2}$AB,
∴PB=$\frac{1}{3}$PA或PA=3PB.
点评 此题考查了切线的性质,内角和定理,圆周角定理,以及含30度直角三角形的性质,熟练掌握性质及定理是解本题的关键.

练习册系列答案
相关题目
3.下列图案中轴对称图形是( )
| A. |  | B. |  | C. |  | D. |  |
10.已知x与y互为相反数,那么|x-3+y|的值是( )
| A. | -3 | B. | 0 | C. | 3 | D. | 无法确定 |
8.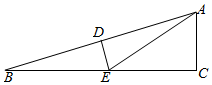 如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6cm,则AC等于( )
如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6cm,则AC等于( )
 如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6cm,则AC等于( )
如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6cm,则AC等于( )| A. | 6cm | B. | 5cm | C. | 4cm | D. | 3cm |
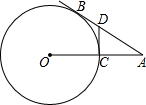 如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,点D在AB上,且DB=DC.
如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,点D在AB上,且DB=DC. 如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且CF=3FD,求证:△ABE∽△DEF.
如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且CF=3FD,求证:△ABE∽△DEF.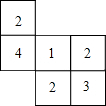 一个几何体由大小相同的小立方块搭成,从上面观察这个几何体看到的形状如图所示,其中小正方形里的数字表示该位置小立方块的个数,请画出从正面、左面看到的这个几何体的形状图.
一个几何体由大小相同的小立方块搭成,从上面观察这个几何体看到的形状如图所示,其中小正方形里的数字表示该位置小立方块的个数,请画出从正面、左面看到的这个几何体的形状图.