题目内容
6. 如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且CF=3FD,求证:△ABE∽△DEF.
如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且CF=3FD,求证:△ABE∽△DEF.
分析 由正方形的性质得出∠A=∠D=90°,AB=AD=CD,设AB=AD=CD=4a,得出AE=DE=2a,DF=a,证出$\frac{AB}{DE}=\frac{AE}{DF}$,即可得出结论.
解答 证明:∵四边形ABCD为正方形,
∴∠A=∠D=90°,AB=AD=CD,
设AB=AD=CD=4a,
∵E为边AD的中点,CF=3FD,
∴AE=DE=2a,DF=a,
∴$\frac{AB}{DE}=\frac{4a}{2a}$=2,$\frac{AE}{DF}=\frac{2a}{a}$=2,
∴$\frac{AB}{DE}=\frac{AE}{DF}$,
又∵∠A=∠D,
∴△ABE∽△DEF.
点评 本题考查了正方形的性质、相似三角形的判定与性质;熟练掌握正方形的性质,熟记两边成比例且夹角相等的两个三角形相似是解题的关键.

练习册系列答案
相关题目
17.下列各组数是勾股数的是( )
| A. | 5,12,13 | B. | 4,5,6 | C. | 7,12,13 | D. | 9,12,13 |
11.在仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱从三个方向看到的图形画了出来,如图所示,则这堆正方体货箱共有( )
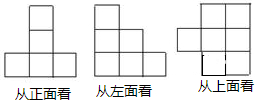

| A. | 9箱 | B. | 10箱 | C. | 11箱 | D. | 12箱 |
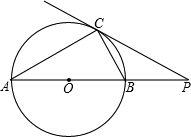 已知:如图,点P在⊙O外,PC是⊙O的切线,C为切点,直线PO与⊙O相交于点A、B.
已知:如图,点P在⊙O外,PC是⊙O的切线,C为切点,直线PO与⊙O相交于点A、B.