题目内容
8.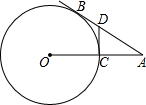 如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,点D在AB上,且DB=DC.
如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,点D在AB上,且DB=DC.(1)求证:DC为⊙O的切线;
(2)若AD=2BD,CD=2,求⊙O的半径.
分析 (1)连接OB、OD,证明OB⊥AB,再证△OBD≌△OCD,证得∠OBD=∠OCD=90°,即可证得结论;
(2)根据题意求得AD=2DC,即可证得∠A=30°,求得AB=6,然后解直角三角形AOB即可求得半径OB.
解答 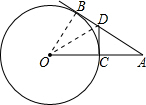 (1)证明:连接OB、OD,
(1)证明:连接OB、OD,
∵AB是⊙O的切线,切点为B,
∴OB⊥AB,
在△OBD和△OCD中,
$\left\{\begin{array}{l}{OB=OC}\\{OD=OD}\\{BD=CD}\end{array}\right.$,
∴△OBD≌△OCD(SSS),
∴∠OCD=∠OBD=90°,
∴DC为⊙O的切线;
(2)解:∵DB=DC,AD=2BD,CD=2,
∴DB=2,AD=4,
∴AB=DB+AD=6,
∵DB=DC,AD=2BD,
∴AD=2DC,
∵DC⊥OC,
∴DC⊥AC,
∴∠A=30°,
在RT△AOB中,tan∠A=$\frac{OB}{AB}$,
∴OB=tan30°×6=$\frac{\sqrt{3}}{3}$×6=2$\sqrt{3}$.
点评 本题考查了切线的判定和性质,三角形全等的判定和性质,解直角三角形等,求得∠A=30°是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.李老师给新入学孩子测量身高,从中抽取10名学生身高数据,其结果(单位:cm)如下:110、97、118、108、111、100、101、96、113、116.为了求得10名学生的平均身高,我们可以选取一个恰当的基准数进行简化运算.
(1)你认为选取的一个恰当的基准数为105;
(2)根据相对身高=实际身高-基准数,结合你选取的基准数,用正、负数填写表格;
(3)这10名学生的平均身高是多少?
| 实际身高/cm | 110 | 97 | 118 | 108 | 111 | 100 | 101 | 96 | 113 | 116 |
| 相对身高/cm |
(2)根据相对身高=实际身高-基准数,结合你选取的基准数,用正、负数填写表格;
(3)这10名学生的平均身高是多少?
17.下列各组数是勾股数的是( )
| A. | 5,12,13 | B. | 4,5,6 | C. | 7,12,13 | D. | 9,12,13 |
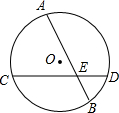 如图,点A、C、B、D在⊙O上,且$\widehat{AB}=\widehat{CD}$,弦AB、CD相交于点E,AE与CE相等吗?为什么?
如图,点A、C、B、D在⊙O上,且$\widehat{AB}=\widehat{CD}$,弦AB、CD相交于点E,AE与CE相等吗?为什么? 有理数a<0、b>0、c>0,且|b|<|a|<|c|,
有理数a<0、b>0、c>0,且|b|<|a|<|c|,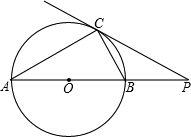 已知:如图,点P在⊙O外,PC是⊙O的切线,C为切点,直线PO与⊙O相交于点A、B.
已知:如图,点P在⊙O外,PC是⊙O的切线,C为切点,直线PO与⊙O相交于点A、B.