题目内容
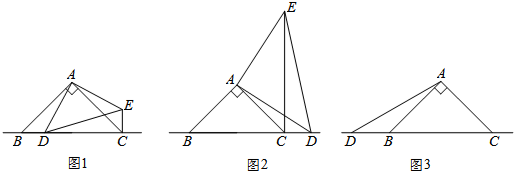
14. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论:①abc<0;②b2-4ac>0;③3a+c>0;④(a+c)2<b2,其中正确的结论为( )
| A. | ①② | B. | ②④ | C. | ①③④ | D. | ①③ |
分析 ①根据抛物线开口向下,得到a<0.由抛物线与y轴交于正半轴,得到c>0.由抛物线对称轴在y轴左侧,b与a同号,得到b<0.于是得到abc>0.故①错误;
②根据抛物线与x轴有两个交点,b2-4ac>0.故②正确.
③当x=-2时,y<0,即4a-2b+c<0 (1),当x=1时,y<0,即a+b+c<0 (2),两式相加即可得到结果;
④由x=1时,y=a+b+c<0,x=-1时,y=a-b+c>0,即可得到结果.故④正确.
解答 解:①∵抛物线开口向下,∴a<0.
又∵抛物线与y轴交于正半轴,∴c>0.
又∵抛物线对称轴在y轴左侧,∴b与a同号,即b<0.
∴abc>0.故①错误.
②∵抛物线与x轴有两个交点,∴b2-4ac>0.故②正确.
③当x=-2时,y<0,即4a-2b+c<0 (1),
当x=1时,y<0,即a+b+c<0 (2),
(1)+(2)×2得:6a+3c<0,即2a+c<0.
又∵a<0,∴a+(2a+c)=3a+c<0.故③错误.
④∵x=1时,y=a+b+c<0,x=-1时,y=a-b+c>0,
∴(a+b+c)(a-b+c)<0,即[(a+c)+b][(a+c)-b]=(a+c)2-b2<0.
∴(a+c)2<b2.故④正确.
综上所述,正确的结论为②④.
故选B.
点评 主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
相关题目
9.2014年天津市全市经济运行情况显示,天津市2014年实现地区生产总值(GDP)15722.47亿元,其中15722.47用科学记数法表示为( )
| A. | 1.572247×105 | B. | 15.72247×103 | C. | 1.572247×104 | D. | 15.72247×102 |
19.2015的倒数是( )
| A. | 2015 | B. | $\frac{1}{2015}$ | C. | -2015 | D. | -$\frac{1}{2015}$ |
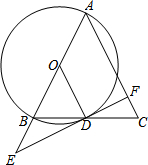 如图,AB是⊙O的直径,以AB为边作△ABC,使得AC=AB,BC交⊙O于点D,联结OD,过点D作⊙O的切线,交AB延长线于点E,交AC于点F.
如图,AB是⊙O的直径,以AB为边作△ABC,使得AC=AB,BC交⊙O于点D,联结OD,过点D作⊙O的切线,交AB延长线于点E,交AC于点F.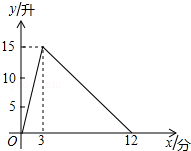 一个有进水管与出水管的容器,从某时刻开始的3分内只进水不出水,在随后的9分内既进水又出水,每分的进水量和出水量都是常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图所示.当容器内的水量大于5升时,时间x的取值范围为1<x<9.
一个有进水管与出水管的容器,从某时刻开始的3分内只进水不出水,在随后的9分内既进水又出水,每分的进水量和出水量都是常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图所示.当容器内的水量大于5升时,时间x的取值范围为1<x<9. 如图,在△ABC中,D、E分别是AB和AC上的点,DE∥BC,AD=3BD,S△ABC=48,求S△ADE的值.
如图,在△ABC中,D、E分别是AB和AC上的点,DE∥BC,AD=3BD,S△ABC=48,求S△ADE的值.