题目内容
19. 如图,在四边形ABCD中,AD∥BC,∠B=90度,AD=18cm,BC=21cm,动点P从A点开始沿AD边向D以1cm/s的速度运动,动点Q从C点开始沿CB边以2cm/s的速度运动,P、Q分别从点A、C同时出发.当其中一点到达端点时,另一点也随之停止运动,设运动的时间为t秒.
如图,在四边形ABCD中,AD∥BC,∠B=90度,AD=18cm,BC=21cm,动点P从A点开始沿AD边向D以1cm/s的速度运动,动点Q从C点开始沿CB边以2cm/s的速度运动,P、Q分别从点A、C同时出发.当其中一点到达端点时,另一点也随之停止运动,设运动的时间为t秒.(1)t为何值时四边形ABQP为矩形?
(2)t为何值时四边形PQCD为平行四边形?
分析 (1)要使得四边形ABQP为矩形,只要AP=BQ即可,从而可以求得此时t的值;
(2)要使得四边形PQCD为平行四边形,只要PD=CQ即可,从而可以求得此时t的值.
解答 解:(1)当AP=BQ时,四边形ABQP为矩形,
∴t=21-2t,
解得,t=7
即当t=7s时,四边形ABQP为矩形;
(2)当PD=CQ时,四边形PQCD为平行四边形,
∴18-t=2t,
解得,t=4.5
即当t=6s时,四边形PQCD为平行四边形.
点评 本题考查矩形的判定、平行四边形的判定,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
10.下列命题:
①若|-$\frac{1}{b}$|=$\frac{1}{b}$,则b≥0;
②若x+y>0,xy<0,x-y<0,则|x|<|y|;
③23与(-3)2不是同类项;
④若|x|+2x=1,则x=$\frac{1}{3}$或x=1.
其中正确的结论有( )
①若|-$\frac{1}{b}$|=$\frac{1}{b}$,则b≥0;
②若x+y>0,xy<0,x-y<0,则|x|<|y|;
③23与(-3)2不是同类项;
④若|x|+2x=1,则x=$\frac{1}{3}$或x=1.
其中正确的结论有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
11.若不等式组$\left\{\begin{array}{l}x-a≥0\\ 1-2x≥x-2\end{array}\right.$有解,则实数a的取值范围是( )
| A. | a<1 | B. | a≤1 | C. | a<0 | D. | a≤0 |
9.下列多项式相乘,不能用平方差公式计算的是( )
| A. | (x-2y)(2y+x) | B. | (2y-x)(-x-2y) | C. | (x-2y)(-x-2y) | D. | (-2y-x)(x+2y) |
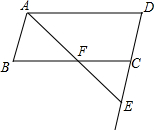 一个平行四边形ABCD,AB=4,BC=9,点E是DC延长线上一点,连接AE交BC边于点F,求BF+EC的最小值.
一个平行四边形ABCD,AB=4,BC=9,点E是DC延长线上一点,连接AE交BC边于点F,求BF+EC的最小值. 如图,直线y=kx-4(k>0)与双曲线y=$\frac{k}{x}$在第一象限内交于点R,与x,y轴的交点分别为P,Q;过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于4$\sqrt{2}$.
如图,直线y=kx-4(k>0)与双曲线y=$\frac{k}{x}$在第一象限内交于点R,与x,y轴的交点分别为P,Q;过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于4$\sqrt{2}$.