题目内容
20.已知抛物线y=x2-2x-3与x轴交于点A,B(点A在点B左侧),其顶点为P,直线y=kx+b过抛物线与x轴的一个交点A,且与抛物线相交的另外一个交点为C,若S△ABC=10,请你回答下列问题:(1)求直线的解析式;
(2)求四边形APBC的面积.
分析 (1)令y=0,则x2-2x-3=0,得到A(-1,0),B(3,0),设C(m,m2-2m-3),根据三角形的面积得到C(4,5)或(-2,5),解方程组即可得到结论;
(2)根据抛物线的解析式得到P(1,-4),根据三角形的面积公式即可得到结论.
解答  解:(1)令y=0,则x2-2x-3=0,
解:(1)令y=0,则x2-2x-3=0,
解得:x1=-1,x2=3,
∴A(-1,0),B(3,0),
设C(m,m2-2m-3),
∴S△ABC=$\frac{1}{2}$×4×|m2-2m-3|=10,
∴m=4或m=-2,
∴C(4,5)或(-2,5),
∴$\left\{\begin{array}{l}{0=-k+b}\\{5=4k+b}\end{array}\right.$或$\left\{\begin{array}{l}{0=-k+b}\\{5=-2k+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$或$\left\{\begin{array}{l}{k=-5}\\{b=-5}\end{array}\right.$,
∴直线的解析式为:y=x+1或y=-5x-5;
(2)如图,∵y=x2-2x-3=(x-1)2-4,
∴P(1,-4),
∵A(-1,0),B(3,0),
∴四边形APBC的面积=S△ABC+S△ABP=$\frac{1}{2}$×4×5+$\frac{1}{2}$×4×4=18.
点评 本题考查了二次函数的图象的性质的运用,三角形的面积公式的运用,梯形的面积公式的运用,抛物线与x轴的交点坐标的运用,解答时求出点C的坐标是关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
11.方程x2=4的解是( )
| A. | x1=4,x2=-4 | B. | x1=x2=2 | C. | x1=2,x2=-2 | D. | x1=1,x2=4 |
 在直径为200cm的圆柱形油槽内装入一些油以后,截面如图.若油面的宽AB=160cm,求油的最大深度.
在直径为200cm的圆柱形油槽内装入一些油以后,截面如图.若油面的宽AB=160cm,求油的最大深度.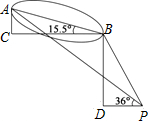 有“小蛮腰”之称的广州电视塔为中国第一高电视塔,其主体顶部450~454米处有世界最高摩天轮(即图中AC=4米),与一般竖立的摩天轮不一样,广州塔的摩天轮沿着倾斜的轨道运转,对地倾斜角为∠ABC=15.5°.小明操作无人机观察摩天轮,由于设备限制无法近距离拍摄,无人机在图中P点观察到摩天轮最低点B的仰角为∠BPD=60°,最高点A的仰角为∠APD=36°,请问此时无人机距离电视塔的水平距离PD为( )(参考数据:tan15.5°≈0.4,tan36°≈0.7,$\sqrt{3}$≈1.7)
有“小蛮腰”之称的广州电视塔为中国第一高电视塔,其主体顶部450~454米处有世界最高摩天轮(即图中AC=4米),与一般竖立的摩天轮不一样,广州塔的摩天轮沿着倾斜的轨道运转,对地倾斜角为∠ABC=15.5°.小明操作无人机观察摩天轮,由于设备限制无法近距离拍摄,无人机在图中P点观察到摩天轮最低点B的仰角为∠BPD=60°,最高点A的仰角为∠APD=36°,请问此时无人机距离电视塔的水平距离PD为( )(参考数据:tan15.5°≈0.4,tan36°≈0.7,$\sqrt{3}$≈1.7)