题目内容
16.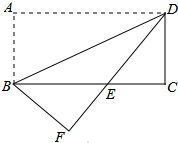 如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.(1)求证:△DCE≌△BFE;
(2)若CD=$\sqrt{3}$,DB=2$\sqrt{3}$,求BE的长.
分析 (1)由矩形的性质可知AB=DC,∠A=∠C=90°,由翻折的性质可知∠AB=BF,∠A=∠F=90°,于是可得到∠F=∠C,BF=DC,然后依据AAS可证明△DCE≌△BFE;
(2)先依据勾股定理求得BC的长,由全等三角形的性质可知BE=DE,最后再△EDC中依据勾股定理可求得ED的长,从而得到BE的长.
解答 (1)∵四边形ABCD为矩形,
∴AB=CD,∠A=∠C=90°
∵由翻折的性质可知∠F=∠A,BF=AB,
∴BF=DC,∠F=∠C.
在△DCE与△BEF中,
$\left\{{\begin{array}{l}{∠F=∠C}\\{BF=CD}\\{∠BEF=∠DEC}\end{array}}\right.$
∴△DCE≌△BFE.
(2)在Rt△BDC中,由勾股定理得:BC=$\sqrt{D{B}^{2}-C{D}^{2}}$=3.
∵△DCE≌△BFE,
∴BE=DE.
设BE=DE=x,则EC=3-x.
在Rt△CDE中,CE2+CD2=DE2,即(3-x)2+($\sqrt{3}$)2=x2.
解得:x=2.
∴BE=2.
点评 本题主要考查的是翻折的性质、勾股定理的应用、矩形的性质,依据勾股定理列出关于x的方程是解题的关键.

练习册系列答案
相关题目
16.已知两点M(3,2),N(-1,3),点P是x轴上一动点,若使PM+PN最短,则点P的坐标应为( )
| A. | (0,$-\frac{7}{4}$) | B. | ($\frac{7}{4}$,0) | C. | ($\frac{3}{2}$,0) | D. | ($\frac{7}{5}$,0) |
5.分解因式8a2-8ab+2b2结果正确的是( )
| A. | 2(2a-b)2 | B. | 8(a-b)2 | C. | 4(a-b)2 | D. | 2(2a+b)2 |
 如图,已知 AB∥CD∥EF,AB:CD:EF=2:3:5,$\overrightarrow{BF}$=$\overrightarrow{a}$,
如图,已知 AB∥CD∥EF,AB:CD:EF=2:3:5,$\overrightarrow{BF}$=$\overrightarrow{a}$,

 如图,BC=EF,∠1=∠F.请你添加一个适当的条件AC=DF,使得△ABC≌△DEF(只需填一个答案即可).
如图,BC=EF,∠1=∠F.请你添加一个适当的条件AC=DF,使得△ABC≌△DEF(只需填一个答案即可).