题目内容
16.已知两点M(3,2),N(-1,3),点P是x轴上一动点,若使PM+PN最短,则点P的坐标应为( )| A. | (0,$-\frac{7}{4}$) | B. | ($\frac{7}{4}$,0) | C. | ($\frac{3}{2}$,0) | D. | ($\frac{7}{5}$,0) |
分析 先求得M的对称点M′的坐标,根据两点的坐标代入一次函数解析式中,确定一次函数解析式,然后根据点P在x轴上,则其纵坐标是0,求出横坐标即可.
解答 解:作M点关于x轴的对称点M′,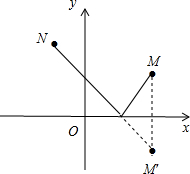
∵M(3,2),
∴M′(3,-2),
设直线M′N的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{3k+b=-2}\\{-k+b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{5}{4}}\\{b=\frac{7}{4}}\end{array}\right.$,
∴直线M′N的解析式为y=-$\frac{5}{4}$x+$\frac{7}{4}$,
∵P的纵坐标为0,
∴-$\frac{5}{4}$x+$\frac{7}{4}$=0,解得x=$\frac{7}{5}$,
∴P($\frac{7}{5}$,0).
故选D.
点评 此题考查了最短路径问题和用待定系数法求一次函数解析式,判断出M、P、N三点共线时MN最小是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.要使分式$\frac{1}{x-1}$有意义,则x的取值范围是( )
| A. | x=1 | B. | x≠1 | C. | x=-1 | D. | x≠-1 |
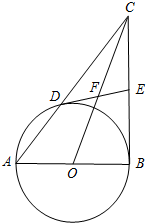 如图,在Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,E是BC的中点,连结DE.
如图,在Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,E是BC的中点,连结DE.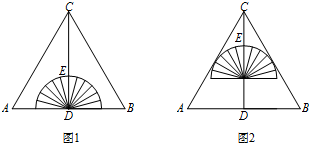
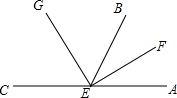 如图,EF、EG分别是∠AEB、∠BEC的平分线,求∠GEF的度数.
如图,EF、EG分别是∠AEB、∠BEC的平分线,求∠GEF的度数.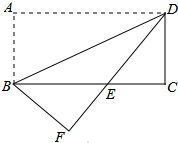 如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.