题目内容
16.先化简,再求值:(x-1-$\frac{3}{x+1}$)÷$\frac{{x}^{2}+4x+4}{x+1}$,其中x=-$\frac{5}{2}$.分析 先化简括号内的式子,然后将除法转化为乘法即可化简题目中的式子,然后将x的值代入化简后的式子即可解答本题.
解答 解:(x-1-$\frac{3}{x+1}$)÷$\frac{{x}^{2}+4x+4}{x+1}$
=$\frac{(x-1)(x+1)-3}{x+1}×\frac{x+1}{(x+2)^{2}}$
=$\frac{{x}^{2}-4}{x+1}×\frac{x+1}{(x+2)^{2}}$
=$\frac{(x+2)(x-2)}{x+1}×\frac{x+1}{(x+2)^{2}}$
=$\frac{x-2}{x+2}$,
当x=-$\frac{5}{2}$时,原式=$\frac{-\frac{5}{2}-2}{-\frac{5}{2}+2}=9$.
点评 本题考查分式的化简求值,解答此类问题的关键是明确分式化简求值的方法.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
7.下列对二次函数y=2(x+4)2的增减性描述正确的是( )
| A. | 当x>0时,y随x的增大而增大 | B. | 当x<0时,y随x的增大而增大 | ||
| C. | 当x>-4时,y随x的增大而减少 | D. | 当x<-4时,y随x的增大而减少 |
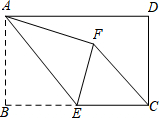 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为$\frac{18}{5}$.
如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为$\frac{18}{5}$.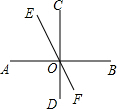 已知:AB⊥CD于O点,直线E过O点,∠EOC=15°,求∠BOF的度数.
已知:AB⊥CD于O点,直线E过O点,∠EOC=15°,求∠BOF的度数. 如图,一只蚂蚁从点A沿圆柱表面爬到点B,如果圆柱的高为8cm,圆柱的底面半径为$\frac{6}{π}$cm,那么蚂蚁爬行的最短的路线长是多少?
如图,一只蚂蚁从点A沿圆柱表面爬到点B,如果圆柱的高为8cm,圆柱的底面半径为$\frac{6}{π}$cm,那么蚂蚁爬行的最短的路线长是多少?