Question

6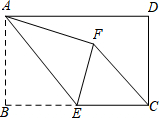．如图，在矩形ABCD中，AB=4，BC=6，点E为BC的中点，将△ABE沿AE折叠，使点B落在矩形内点F处，连接CF，则CF的长为$\frac{18}{5}$．

Answer 1

分析 连接BF，根据三角形的面积公式求出BH，得到BF，根据直角三角形的判定得到∠BFC=90°，根据勾股定理求出答案．

解答 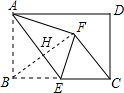解：连接BF，
∵BC=6，点E为BC的中点，
∴BE=3，
又∵AB=4，
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=5，
∴BH=$\frac{12}{5}$，
则BF=$\frac{24}{5}$，
∵FE=BE=EC，
∴∠BFC=90°，
∴CF=$\sqrt{{6}^{2}-（\frac{24}{5}）^{2}}$=$\frac{18}{5}$．
故答案为：$\frac{18}{5}$．

点评 本题考查的是翻折变换的性质和矩形的性质，掌握折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等是解题的关键．