题目内容
18.一列火车从甲站开出,到相距450千米的乙站,当它开出了3小时后,因特殊任务多停一站,耽误30分钟,然后把速度提高到原来的1.2倍,结果准时到达目的地,求这列火车原来的速度.分析 如果设这列火车原来的速度为每小时x千米,那么提速后的速度为每小时1.2x千米,根据等量关系:按原速度行驶所用时间-提速后时间=$\frac{1}{2}$,列出方程,求解即可.
解答 解:设这列火车原来的速度为每小时x千米.
由题意得:$\frac{450-3x}{x}$-$\frac{450-3x}{1.2x}$=$\frac{1}{2}$.
整理得:12x=900.
解得:x=75.
经检验:x=75是原方程的解.
答:这列火车原来的速度为每小时75千米.
点评 本题考查分式方程的应用,列分式方程解应用题与所有列方程解应用题一样,重点在于准确地找出相等关系,这是列方程的依据.而难点则在于对题目已知条件的分析,也就是审题,一般来说应用题中的条件有两种,一种是显性的,直接在题目中明确给出,而另一种是隐性的,是以题目的隐含条件给出.如本题:提高到原来的1.2倍,是一种隐含条件.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
17.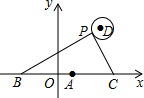 如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是( )
如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是( )
 如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是( )
如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
6.某商店售货时,在进价基础上加一定利润,其数量x与售价y如下表所示,则售价y与数量x的函数关系式为( )
| 数量x(千克) | 1 | 2 | 3 | 4 | … |
| 售价y(元) | 8+0.4 | 16+0.8 | 24+1.2 | 32+1.6 | … |
| A. | y=8+0.4x | B. | y=8x+0.4 | C. | y=8.4x | D. | y=8.4x+0.4 |
7.若(a2+2a+1)2+|1-b|=0,则ab的值是( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 2 |
 (1)如图,请用尺规作图法,确定出图中残缺的圆形铁片的圆心.
(1)如图,请用尺规作图法,确定出图中残缺的圆形铁片的圆心. 已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(-6,0),B点坐标为(4,0),点D为BC的中点,点E为线段AB上一动点.经过点A、B、C三点的抛物线的解析式为y=ax2+bx+8.
已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(-6,0),B点坐标为(4,0),点D为BC的中点,点E为线段AB上一动点.经过点A、B、C三点的抛物线的解析式为y=ax2+bx+8.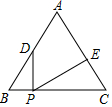 如图,在等边三角形ABC中,BC=8,点D是边AB上一点,且BD=3,点P是边BC上一动点,作∠DPE=60°,PE交边AC于点E,当CE=$\frac{16}{3}$时,满足条件的点P有且只有一个.
如图,在等边三角形ABC中,BC=8,点D是边AB上一点,且BD=3,点P是边BC上一动点,作∠DPE=60°,PE交边AC于点E,当CE=$\frac{16}{3}$时,满足条件的点P有且只有一个. 如图,CD是⊙O的直径,CD=4,∠ACD=20°,点B为弧AD 的中点,点P是直径CD 上的一个动点,则PA+PB的最小值为2.
如图,CD是⊙O的直径,CD=4,∠ACD=20°,点B为弧AD 的中点,点P是直径CD 上的一个动点,则PA+PB的最小值为2.