题目内容
16．计算：$\sqrt{12}-2tan{60°}+{（\sqrt{2015}-1）^0}-{（\frac{1}{3}）^{-1}}$．分析 分别利用算术平方根以及负整数指数幂的性质以及零指数幂的性质和特殊角的三角函数值化简求出即可．
解答 解：原式=2$\sqrt{3}$-2$\sqrt{3}$+1-3
=-2．
点评 此题主要考查了算术平方根以及负整数指数幂的性质以及零指数幂的性质和特殊角的三角函数值等知识，正确化简各数是解题关键．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
6．
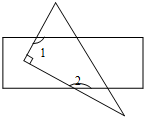如图，将一张矩形纸片和一张直角三角形纸片叠放在一起，∠1+∠2的值是（ ）
如图，将一张矩形纸片和一张直角三角形纸片叠放在一起，∠1+∠2的值是（ ）| A． | 180° | B． | 240° | C． | 270° | D． | 300° |
4．一个不透明的口袋中，装有5个红球，2个黄球，1个白球，这些球除颜色外其余都相同，从口袋中随机摸一个球，则摸到红球的概率为（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{3}{8}$ | C． | $\frac{5}{8}$ | D． | $\frac{3}{4}$ |
11．
2015年是中国抗日战争胜利70周年暨世界反法西斯战争胜利70周年．某校为纪念中国抗日战争胜利70周年，对全校学生进行了“抗日战争知多少”知识测验．然后随机抽取了部分学生的成绩，整理并制作如图所示的图表．
请你根据图表中提供的信息，解答下列问题：
（1）在频数分布表中：m=0.3，n=120；
（2）补全频数分布直方图；
（3）如果某校有2000名学生，比赛成绩80分以上为优秀，那么你估计此次测验成绩的优秀人数大约是1200人．
2015年是中国抗日战争胜利70周年暨世界反法西斯战争胜利70周年．某校为纪念中国抗日战争胜利70周年，对全校学生进行了“抗日战争知多少”知识测验．然后随机抽取了部分学生的成绩，整理并制作如图所示的图表．请你根据图表中提供的信息，解答下列问题：
| 分数段 | 频数 | 频率 |
| 60≤x＜70 | 30 | 0.1 |
| 70≤x＜80 | 90 | m |
| 80≤x＜90 | n | 0.4 |
| 90≤x＜100 | 60 | 0.2 |
（2）补全频数分布直方图；
（3）如果某校有2000名学生，比赛成绩80分以上为优秀，那么你估计此次测验成绩的优秀人数大约是1200人．
8．
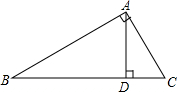如图，Rt△ABC中，∠BAC=90°，AD⊥BC于D，设∠ABC=α，则下列结论错误的是（ ）
如图，Rt△ABC中，∠BAC=90°，AD⊥BC于D，设∠ABC=α，则下列结论错误的是（ ）| A． | BC=$\frac{AC}{sinα}$ | B． | CD=AD•tanα | C． | BD=ABcosα | D． | AC=ADcosα |
5．
如图，在△ABC中，已知AB=AC，DE垂直平分AC，且AC=8，BC=6，则△BDC的周长为（ ）
如图，在△ABC中，已知AB=AC，DE垂直平分AC，且AC=8，BC=6，则△BDC的周长为（ ）| A． | 20 | B． | 22 | C． | 10 | D． | 14 |
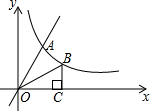如图，直线y=2x与反比例函数y=$\frac{k}{x}$（k≠0，x＞0）的图象交于点A（1，a），点B是此反比例函数图形上任意一点（不与点A重合），BC⊥x轴于点C．