题目内容
8.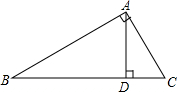 如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,设∠ABC=α,则下列结论错误的是( )
如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,设∠ABC=α,则下列结论错误的是( )| A. | BC=$\frac{AC}{sinα}$ | B. | CD=AD•tanα | C. | BD=ABcosα | D. | AC=ADcosα |
分析 在直角三角形中利用锐角三角函数求角边关系即可.
解答 解:A.在Rt△ABC中,sinα=$\frac{AC}{BC}$,
∴BC=$\frac{AC}{sinα}$,故A正确;
B.∵∠B+∠BAD=90°,∠CAD+∠BAD=90°,
∴∠B=∠CAD=α,
在Rt△ADC中,tanα=$\frac{CD}{AD}$,
∴CD=AD•tanα,
故B正确;
C.在Rt△ABD中,
cosα=$\frac{BD}{AB}$,
∴BD=AB•cosα,
故C正确;
D.在Rt△ADC中,cosα=$\frac{AD}{AC}$,
∴AD=AC•cosα,
故D错误;
故选D.
点评 本题主要考查了直角三角形角边关系,熟练掌握边角之间的关系:sinA=∠A的对边斜边=ac,cosA=∠A的邻边斜边=bc,tanA=∠A的对边∠A的邻边=ab.
(a,b,c分别是∠A、∠B、∠C的对边)是解答此题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
3.如图中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.某次歌咏比赛,最后三名选手的成绩统计如下:
若唱功,音乐常识,综合知识按6:3:1的加权平均分排出冠军、亚军、季军、则冠军,亚军,季军分别是
( )
| 测试项目 | 测试成绩 | ||
| 王飞 | 李真 | 林杨 | |
| 唱功 | 98 | 95 | 80 |
| 音乐常识 | 80 | 90 | 100 |
| 综合知识 | 80 | 90 | 100 |
( )
| A. | 王飞、李真、林杨 | B. | 李真、王飞、林杨 | C. | 王飞、林杨、李真 | D. | 李真、林杨、王飞 |
 反比例函数y=$\frac{k}{x}$(x>0)的图象经过△OAB的顶点A,已知AO=AB,S△OAB=4,则k的值为( )
反比例函数y=$\frac{k}{x}$(x>0)的图象经过△OAB的顶点A,已知AO=AB,S△OAB=4,则k的值为( )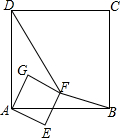 正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连结DF,BF,如图.
正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连结DF,BF,如图. 如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③△GDE∽△BEF;④S△BEF=$\frac{72}{5}$.在以上4个结论中,正确的有( )
如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③△GDE∽△BEF;④S△BEF=$\frac{72}{5}$.在以上4个结论中,正确的有( )