题目内容
6．
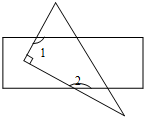如图，将一张矩形纸片和一张直角三角形纸片叠放在一起，∠1+∠2的值是（ ）| A． | 180° | B． | 240° | C． | 270° | D． | 300° |
分析 过B点作BE∥AF，进而可得：AF∥BE∥CD，然后利用平行线的性质即可求出∠1+∠2的值．
解答 解：过B点作BE∥AF，
∵AF∥CD，
∴AF∥BE∥CD，
∴∠1+∠ABE=180°，∠2+∠CBE=180°，
∴∠1+∠ABE+∠CBE+∠2=360°，
∵∠ABE+∠CBE=90°，
∴∠1+∠2=270°．
故选C．
点评 此题考查了平行线的性质，解题的关键是：过B点作BE∥AF，然后利用平行线的性质：两直线平行同旁内角互补解决问题．
练习册系列答案
相关题目
1．当x=5，y=4时，式子x-$\frac{y}{2}$的值是（ ）
| A． | 3 | B． | $\frac{1}{2}$ | C． | -3 | D． | -$\frac{3}{2}$ |
如图，正五边形FGHIJ的顶点在正五边形ABCDE的边上，若∠1=20°，则∠2=52°．
反比例函数y=$\frac{k}{x}$（x＞0）的图象经过△OAB的顶点A，已知AO=AB，S△OAB=4，则k的值为（ ）
15．下列四个数中，-2的倒数是（ ）
| A． | 2 | B． | -2 | C． | 0 | D． | -$\frac{1}{2}$ |