题目内容
17．若代数式3x2-4x-1的值为0，则x2-$\frac{4}{3}x+\frac{2}{3}$=1．分析 首先根据代数式3x2-4x-1的值为0得到3x2-4x-1=0，从而得到x2-$\frac{4}{3}$x=$\frac{1}{3}$，代入代数式即可求解．
解答 解：∵代数式3x2-4x-1的值为0，
∴3x2-4x-1=0，
∴x2-$\frac{4}{3}$x=$\frac{1}{3}$，
∴x2-$\frac{4}{3}x+\frac{2}{3}$═$\frac{1}{3}$$+\frac{2}{3}$=1，
故答案为：1．
点评 本题考查了一元二次方程的解，解题的关键是根据题意得到方程，并进一步求得代数式x2-$\frac{4}{3}$x的值，难度不大．
练习册系列答案
名校课堂系列答案
相关题目
若有理数在数轴上的位置如图所示，则化简：|a+c|+|a-b|-|c+a|=a-b．
如图是一名考古学家发现的一块古代车轮碎片，你能帮他找到这个车轮的半径吗？（画出示意图，保留作图痕迹）
12．把抛物线y=$\frac{1}{2}{x^2}$+1先向右平移1个单位，再向下移2个单位，得到的抛物线解析式是（ ）
| A． | y=$\frac{1}{2}{（{x+1}）^2}$-3 | B． | y=$\frac{1}{2}{（{x-1}）^2}$+3 | C． | y=$\frac{1}{2}{（{x+1}）^2}$-1 | D． | y=$\frac{1}{2}{（{x-1}）^2}$-1 |
2．某种新产品的进价是120元，在试销阶段发现产品的日销售量y（件）与每件售价x（元）存在一次函数关系，部分对应值如下表：
（1）请你根据表中所给数据直接写出日销售量y（件）与每件售价x（元）之间的关系式：y=-x+200，自变量x的取值范围是x≥120
（2）在不改变上述关系的情况下，请你帮助商场经理策划每件商品定价为多少元时，每日盈利可达到1600元．
| 日销售量y（件） | 70 | 50 | 35 |
| 每件售价x（元） | 130 | 150 | 165 |
（2）在不改变上述关系的情况下，请你帮助商场经理策划每件商品定价为多少元时，每日盈利可达到1600元．
6．下列函数图象中，当x＞0时，y随x的增大而减小的是（ ）
| A． | y=-$\frac{1}{x}$ | B． | y=x | C． | y=x2 | D． | y=-（x+1）2 |
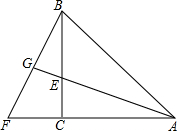如图，在△ABC，∠ACB=90°，BC=AC，AE是△ABC的角平分线，延长AC至点F，使FC=EC，连结BF，延长AE交BF于点G．