题目内容
2.先化简,再求值:$\frac{x+2y}{x+y}$+$\frac{{2y}^{2}}{{x}^{2}{-y}^{2}}$,其中x=-2,y=-1.分析 利用分式的基本性质将原式通分、合并同类项后化简,再代入x=-2,y=-1即可得出结论.
解答 解:原式=$\frac{(x+2y)(x-y)}{(x+y)(x-y)}$+$\frac{2{y}^{2}}{(x+y)(x-y)}$,
=$\frac{{x}^{2}+xy-2{y}^{2}+2{y}^{2}}{(x+y)(x-y)}$,
=$\frac{x(x+y)}{(x+y)(x-y)}$,
=$\frac{x}{x-y}$,
=$\frac{-2}{-2-(-1)}$,
=2.
点评 本题考查了分式的化简求值,解题的关键是:将原式化简为$\frac{x}{x-y}$.本题属于基础题,难度不大,再做形如此类题型时,切记分母不能为0.

练习册系列答案
相关题目
17. 如右图,若AB∥CD,∠1=50°,则∠2的度数是( )
如右图,若AB∥CD,∠1=50°,则∠2的度数是( )
 如右图,若AB∥CD,∠1=50°,则∠2的度数是( )
如右图,若AB∥CD,∠1=50°,则∠2的度数是( )| A. | 50° | B. | 130° | C. | 40° | D. | 145° |
7.已知抛物线y=ax2+bx+c的开口向上,顶点坐标为(3,-2),那么该抛物线有( )
| A. | 最小值-2 | B. | 最大值-2 | C. | 最小值3 | D. | 最大值3 |
 如图:已知AB∥CF,若∠ABC=70°,∠BCD=20°,∠CDE=130°,
如图:已知AB∥CF,若∠ABC=70°,∠BCD=20°,∠CDE=130°,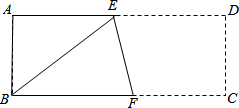 已知,如图长方形ABCD中,AB=a,AD=b,且a、b满足b=$\sqrt{a-3}+\sqrt{6-2a}$+9,将此长方形折叠,使点B与点D重合,折痕为EF,
已知,如图长方形ABCD中,AB=a,AD=b,且a、b满足b=$\sqrt{a-3}+\sqrt{6-2a}$+9,将此长方形折叠,使点B与点D重合,折痕为EF,