题目内容
10.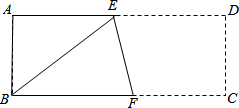 已知,如图长方形ABCD中,AB=a,AD=b,且a、b满足b=$\sqrt{a-3}+\sqrt{6-2a}$+9,将此长方形折叠,使点B与点D重合,折痕为EF,
已知,如图长方形ABCD中,AB=a,AD=b,且a、b满足b=$\sqrt{a-3}+\sqrt{6-2a}$+9,将此长方形折叠,使点B与点D重合,折痕为EF,(1)求a,b的值;
(2)求△ABE的面积;
(3)求折痕为EF的长.
分析 (1)根据二次根式有意义的条件即可解决问题.
(2)设ED=BE=x,在RT△ABE中利用勾股定理求出x,即可解决问题.
(3)连接BD交EF于O,只要证明EF=2EO,在RT△EDO中利用勾股定理即可求出EO.
解答 解:(1)∵ b=$\sqrt{a-3}+\sqrt{6-2a}$+9,
b=$\sqrt{a-3}+\sqrt{6-2a}$+9,
∴a-3≥0,6-2a≥0,
∴a=3,b=9.
(2)设ED=EB=x,则AE=9-x,
∵四边形ABCD是长方形,
∴∠A=90°
在RT△ABE中,∵AB2+AE2=BE2,
∴32+(9-x)2=x2,
∴x=5,
∴AE=4,BE=ED=5,
∴S△ABE=$\frac{1}{2}$•AB•AE=$\frac{1}{2}$×3×4=6.
(3)连接BD交EF于O,
∵BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{6}^{2}+{9}^{2}}$=3$\sqrt{13}$,
∴BO=OD=$\frac{3\sqrt{13}}{2}$,
在RT△EOD中,EO=$\sqrt{E{D}^{2}-D{O}^{2}}$=$\frac{\sqrt{17}}{2}$,
∵DA∥CB,
∴$\frac{EO}{OF}=\frac{DO}{BO}$=1,
∴EO=OF,
∴EF=2EO=$\sqrt{17}$.
点评 本题考查翻折变换、非负数的性质、勾股定理等知识,解题关键是利用翻折不变性,设未知数利用勾股定理列出方程解决,学会转化的思想,属于中考常考题型.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
1.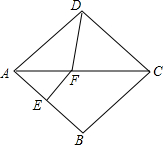 如图所示,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
如图所示,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
 如图所示,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
如图所示,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )| A. | 75° | B. | 70° | C. | 60° | D. | 55° |
18.正方形的边长是2,它的对角线长为( )
| A. | 1 | B. | 2$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
15.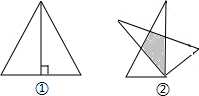 如图,将一个边长为2cm的等边三角形沿去高线剪成两个直角三角形,然后将其中一个直角三角形绕其直角顶点逆时针旋转30°,则阴影部分的周长为( )
如图,将一个边长为2cm的等边三角形沿去高线剪成两个直角三角形,然后将其中一个直角三角形绕其直角顶点逆时针旋转30°,则阴影部分的周长为( )
 如图,将一个边长为2cm的等边三角形沿去高线剪成两个直角三角形,然后将其中一个直角三角形绕其直角顶点逆时针旋转30°,则阴影部分的周长为( )
如图,将一个边长为2cm的等边三角形沿去高线剪成两个直角三角形,然后将其中一个直角三角形绕其直角顶点逆时针旋转30°,则阴影部分的周长为( )| A. | ($\sqrt{3}$-1)cm | B. | 2cm | C. | ($\sqrt{3}$+1)cm | D. | 无法确定 |