题目内容
13. 如图:已知AB∥CF,若∠ABC=70°,∠BCD=20°,∠CDE=130°,
如图:已知AB∥CF,若∠ABC=70°,∠BCD=20°,∠CDE=130°,(1)求∠DCF的度数.
(2)求证:DE∥CF.
分析 (1)由平行线的性质得出内错角相等∠BCF=∠ABC=70°,得出∠DCF=∠BCF-∠BCD=50°即可;
(2)由∠DCF+∠CDE=180°,即可得出结论DE∥CF.
解答 (1)解:∵AB∥CF,
∴∠BCF=∠ABC=70°,
∵∠BCD=20°,
∴∠DCF=∠BCF-∠BCD=50°;
(2)证明:∵∠DCF=50°,∠CDE=130°,
∴∠DCF+∠CDE=180°,
∴DE∥CF.
点评 本题主要考查平行线的判定与性质;熟记平行线的性质和判定是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
相关题目
3.下列说法中,正确的是( )
| A. | -1,3,5,-2,2,-1这组数据的方差是7 | |
| B. | 用长分别为2cm,3cm,5cm的线围成三角形是必然事件 | |
| C. | “嫦娥三号”发射前,对其零部件应抽取一部分进行检查 | |
| D. | 茗茗上学经过十字路口遇到红灯时随机事件 |
1.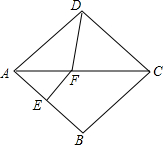 如图所示,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
如图所示,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
 如图所示,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
如图所示,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )| A. | 75° | B. | 70° | C. | 60° | D. | 55° |
18.正方形的边长是2,它的对角线长为( )
| A. | 1 | B. | 2$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
 如图,已知Rt△AOB中,∠AOB=90°,AO=5,BO=3,点E、M是线段AB上的两个不同的动点(不与端点重合),分别过E、M作AO的垂线,垂足分别为K、L.
如图,已知Rt△AOB中,∠AOB=90°,AO=5,BO=3,点E、M是线段AB上的两个不同的动点(不与端点重合),分别过E、M作AO的垂线,垂足分别为K、L.