题目内容
11.已知,AB∥CD,点P为AB、CD之间一点,连接AC.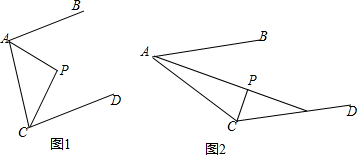
(1)如图1,若AP平分∠BAC,CP平分∠ACD,求证:AP⊥CP;
(2)如图2,若∠PCD=2∠BAP,∠APC=90°,∠ACP=5∠PAC,延长AP交CD于点E,试探究∠PAC与∠AEC之间的数量关系,并说明理由.
(注意:本题不允许使用三角形内角和为180°)
分析 (1)过点P作PE∥AB,由AB∥CD,可得AB∥PE∥CD,再根据平行线的性质可得∠BAP=∠APE,∠DCP=∠CPE,再由角平分线的性质可得∠BAP=$\frac{1}{2}$∠BAC,∠DCP=$\frac{1}{2}$∠ACD,由AB∥CD可得∠BAC+∠ACD=180°,进而可得∠APE+∠CPE=90°,进而可得AP⊥CP;
(2)由(1)可得∠APC=∠BAP+∠DCP,由∠PCD=2∠BAP,∠APC=90°可得∠BAP的度数,进而可得∠PCD的度数,再根据∠ACP=5∠PAC计算出∠PAC=15°,再根据AB∥CD,可得∠BAP=∠AEC=30°,进而可得2∠PAC=∠AEC.
解答 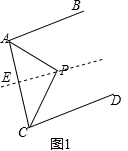 解:(1)过点P作PE∥AB,
解:(1)过点P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠BAP=∠APE,∠DCP=∠CPE,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵AP平分∠BAC,CP平分∠ACD,
∴∠BAP=$\frac{1}{2}$∠BAC,∠DCP=$\frac{1}{2}$∠ACD,
∴∠APC=∠APE+∠CPE=∠BAP+∠DCP=$\frac{1}{2}$(∠BAC+∠ACD)=90°,
∴AP⊥CP;
(2)2∠PAC=∠AEC,
同(1)可证∠APC=∠BAP+∠DCP,
∵∠PCD=2∠BAP,∠APC=90°,
∴∠BAP+2∠BAP=90°,
∴∠BAP=30°,∠PCD=60°,
∵∠BAC+∠ACD=180°,
∴∠ACP+∠PAC=90°,
∵∠ACP=5∠PAC,
∴5∠PAC+∠PAC=90°,
∴∠PAC=15°,
∵AB∥CD,
∴∠BAP=∠AEC=30°,
∴2∠CAP=∠AEC.
点评 此题主要考查了平行线的性质,以及角平分线的性质,关键是正确理清图中角之间的关系,掌握两直线平行,同旁内角相等.

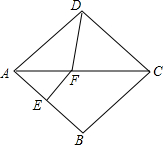 如图所示,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
如图所示,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )| A. | 75° | B. | 70° | C. | 60° | D. | 55° |
| A. | ab>ac | B. | a+b>b+c | C. | a-b>b-c | D. | $\frac{a}{c}$>$\frac{b}{c}$ |
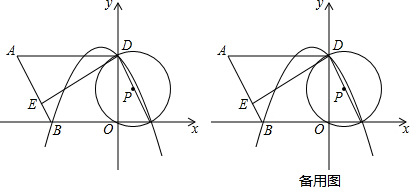
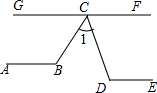 如图,AB∥DE∥GF,∠1:∠D:∠B=2:3:4,求∠1的度数?
如图,AB∥DE∥GF,∠1:∠D:∠B=2:3:4,求∠1的度数? 如图,已知Rt△AOB中,∠AOB=90°,AO=5,BO=3,点E、M是线段AB上的两个不同的动点(不与端点重合),分别过E、M作AO的垂线,垂足分别为K、L.
如图,已知Rt△AOB中,∠AOB=90°,AO=5,BO=3,点E、M是线段AB上的两个不同的动点(不与端点重合),分别过E、M作AO的垂线,垂足分别为K、L.