题目内容
15.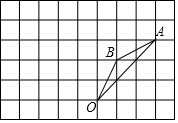 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,3)、B(1,2),△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,3)、B(1,2),△AOB绕点O逆时针旋转90°后得到△A1OB1.(1)画出△A1OB1,直接写出点A1,B1的坐标;
(2)求在旋转过程中,线段AB所扫过的面积.
分析 (1)根据网格结构找出点A、B绕点O逆时针旋转90°后的对应点A1、B1的位置,然后顺次连接即可,再根据平面直角坐标系写出各点的坐标;
(2)根据AB扫过的面积等于以OA、OB为半径的两个扇形的面积的差列式计算即可得解.
解答 解:(1)如图,△A1OB1即为所求三角形,A1(-3,3),B1(-2,1);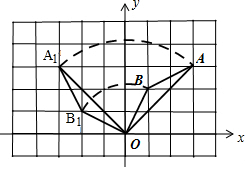
(2)∵OB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,OA=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
∴S扇形OAA1=$\frac{90•π•(3\sqrt{2})^{2}}{360}$=$\frac{9}{2}$π,
S扇形OBB1=$\frac{90•π•(\sqrt{5})^{2}}{360}$=$\frac{5}{4}$π,
则线段AB所扫过的面积为:$\frac{9}{2}$π-$\frac{5}{4}$π=$\frac{13}{4}$π.
点评 本题考查利用旋转变换作图,扇形的面积,熟练掌握网格结构,准确找出对应点的位置是解题的关键,判断出AB扫过的面积等于两个扇形的面积的差是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.今年是中国工农红军长征胜利80周年,我校为了了解学生对“红军长征历史”的知晓情况,从全校1600名学生中随机抽取了100名学生进行调查.在这次调查中,样本是( )
| A. | 1600名学生 | |
| B. | 100名学生 | |
| C. | 所抽取的100名学生对“红军长征历史”的知晓情况 | |
| D. | 每一名学生对“红军长征历史”的知晓情况 |
7. 如图,已知DE是△ABC的中位线,则△ADE的面积:四边形DBCE的面积是( )
如图,已知DE是△ABC的中位线,则△ADE的面积:四边形DBCE的面积是( )
 如图,已知DE是△ABC的中位线,则△ADE的面积:四边形DBCE的面积是( )
如图,已知DE是△ABC的中位线,则△ADE的面积:四边形DBCE的面积是( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:8 |
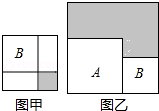 有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为2和13,则正方形A,B的面积之和为15.
有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为2和13,则正方形A,B的面积之和为15.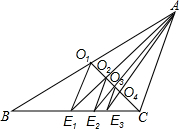 如图,已知CO1是△ABC的中线,过点O1作O1E1∥AC交BC于点E1,连接AE1交CO1于点O2;过点O2作O2E2∥AC交BC于点E2,连接AE2交CO1于点O3;过点O3作O3E3∥AC交BC于点E3,…,如此继续,可以依次得到点O4,O5,…,On和点E4,E5,…,En,则O2016E2016=$\frac{1}{2017}$AC.
如图,已知CO1是△ABC的中线,过点O1作O1E1∥AC交BC于点E1,连接AE1交CO1于点O2;过点O2作O2E2∥AC交BC于点E2,连接AE2交CO1于点O3;过点O3作O3E3∥AC交BC于点E3,…,如此继续,可以依次得到点O4,O5,…,On和点E4,E5,…,En,则O2016E2016=$\frac{1}{2017}$AC. 如图,AB为⊙O的直径,E为⊙O上一点,∠EAB的平分线AC交⊙O于C点,过C点作CD⊥AE交AE的延长线于D点,直线CD与射线AB交于P点.
如图,AB为⊙O的直径,E为⊙O上一点,∠EAB的平分线AC交⊙O于C点,过C点作CD⊥AE交AE的延长线于D点,直线CD与射线AB交于P点.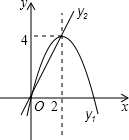 如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1=y2,记M=y1=y2,下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的有( )
如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1=y2,记M=y1=y2,下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的有( )