题目内容
19．
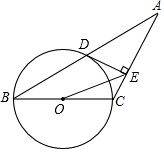如图，已知等腰三角形ABC的底角为30°，以腰BC为直径的⊙O与底边AB交于点D，过点D作DE⊥AC，垂足为E．求证：DE为⊙O的切线．
分析 连接OD，根据等腰三角形的性质得到∠ACB=∠DOB=120°，得到OD∥AC，得到∠ODE=90°，根据切线的判定定理证明结论．
解答 证明：连接OD，
∵CA=CB，OB=OD，∠B=30°，
∴∠ACB=∠DOB=120°，
∴OD∥AC，又DE⊥AC，
∴∠ODE=∠CED=90°，
∴DE为⊙O的切线．
点评 本题考查的是切线的判定、等腰三角形的性质，掌握经过半径的外端且垂直于这条半径的直线是圆的切线是解题的关键．
练习册系列答案
相关题目
小明发现：作两条互相垂直的直线MN、PQ，垂足为O，作∠PON的角平分线OE，点A、B分别是OE、PQ上任意一点，再作∠ABP的平分线BD，BD的反向延长线交∠OAB的平分线于点C，∠C的大小是不随A、B的变化而变化的，是一个定值，∠C为22.5°．
7．
如图，已知DE是△ABC的中位线，则△ADE的面积：四边形DBCE的面积是（ ）
如图，已知DE是△ABC的中位线，则△ADE的面积：四边形DBCE的面积是（ ）| A． | 1：2 | B． | 1：3 | C． | 1：4 | D． | 1：8 |
14．某检修小组从A地出发，在东西向的铁路上检修线路，如果规定向东行驶为正，向西行驶为负，一天中六次行驶情况记录如下（单位：公里）
（1）求这天结束时距A地多远？
（2）若每公里耗油1.2升，问共耗油多少升？
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 |
| -5 | +7 | -9 | +10 | +6 | -5 |
（2）若每公里耗油1.2升，问共耗油多少升？
如图，AB为⊙O的直径，E为⊙O上一点，∠EAB的平分线AC交⊙O于C点，过C点作CD⊥AE交AE的延长线于D点，直线CD与射线AB交于P点．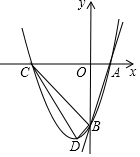
如图，已知直线y=3x-3分别交x轴，y轴于A，B两点，抛物线y=x2+bx+c经过A，B两点，点C是抛物线与x轴的另一个交点（与点A不重合），点D是抛物线的顶点，请解答下列问题．