题目内容
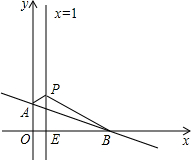 如图,平面直角坐标系中,直线AB:y=-
如图,平面直角坐标系中,直线AB:y=-| 3 |
| 4 |
(1)直接写出A、B的坐标;A
(2)是否存在点P,使得△AOP的周长最小?若存在,请求出周长的最小值;若不存在,请说明理由.
(3)是否存在点P使得△ABP是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)根据自变量与函数值相应的关系,由自变量的值,可得相应的函数值,根据函数值,可得相应自变量的值;
(2)根据线段垂直平分线的性质,可得PO=PM,根据两点之间线段最短,可得AP+PO=AP+PM=AM,再根据三角形的周长,可得答案;
(3)根据等腰三角形的定义,可得两边分别相等,分类讨论:①AP=BP,②当AP=AB=5,③当BP=AB=5,根据两点间的距离,可得关于a的方程,根据解方程,可得答案.
(2)根据线段垂直平分线的性质,可得PO=PM,根据两点之间线段最短,可得AP+PO=AP+PM=AM,再根据三角形的周长,可得答案;
(3)根据等腰三角形的定义,可得两边分别相等,分类讨论:①AP=BP,②当AP=AB=5,③当BP=AB=5,根据两点间的距离,可得关于a的方程,根据解方程,可得答案.
解答:解:(1)当x=0时,y=3.即A 点坐标是(0,3),
当y=0时,-
x+3=0,解得x=4,即B点坐标是(4,0);
(2)存在这样的P,使得△AOP周长最小
作点O关于直线x=1的对称点M,
M点坐标(2,0)连接AM交直线x=1于点P,
由勾股定理,得AM=
=
=
由对称性可知OP=MP,C△AOP=AO+OP+AP=AO+MP+AP=AO+AM=3+
=
+3;
(3)设P点坐标为(1,a),
①当AP=BP时,两边平方得,AP2=BP2,12+(a-3)2=(1-4)2+a2.
化简,得6a=1.
解得a=
.即P1(1,
);
②当AP=AB=5时,两边平方得,AP2=AB2,12+(a-3)2=52.
化简,得a2-6a-15=0.
解得a=3±2
,即P2(1,3+2
),P3(1,3-2
);
③当BP=AB=5时,两边平方得,BP2=AB2,即(1-4)2+a2=52.
化简,得a2=16.
解得a=±4,即P4(1,4),P5(1,-4).
综上所述:P1(1,
);P2(1,3+2
),P3(1,3-2
);P4(1,4),P5(1,-4).
当y=0时,-
| 3 |
| 4 |
(2)存在这样的P,使得△AOP周长最小
作点O关于直线x=1的对称点M,
M点坐标(2,0)连接AM交直线x=1于点P,
由勾股定理,得AM=
| OA2+OM2 |
| 32+22 |
| 13 |
由对称性可知OP=MP,C△AOP=AO+OP+AP=AO+MP+AP=AO+AM=3+
| 22+32 |
| 13 |
(3)设P点坐标为(1,a),
①当AP=BP时,两边平方得,AP2=BP2,12+(a-3)2=(1-4)2+a2.
化简,得6a=1.
解得a=
| 1 |
| 6 |
| 1 |
| 6 |
②当AP=AB=5时,两边平方得,AP2=AB2,12+(a-3)2=52.
化简,得a2-6a-15=0.
解得a=3±2
| 6 |
| 6 |
| 6 |
③当BP=AB=5时,两边平方得,BP2=AB2,即(1-4)2+a2=52.
化简,得a2=16.
解得a=±4,即P4(1,4),P5(1,-4).
综上所述:P1(1,
| 1 |
| 6 |
| 6 |
| 6 |
点评:本题考查了一次函数的综合题,(1)利用了自变量与函数值的相应关系,可得点的坐标,(2)利用了线段垂直平分线的性质,线段的性质,(3)利用了等腰三角形的定义,解方程,分类讨论是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列图形中,既是轴对称图形,又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
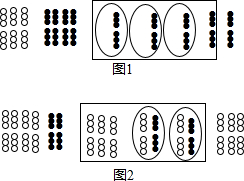 我国是最早认识负数,并进行相关运算的国家.在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算3+(-4)的过程.按照这种方法,图2表示的过程应是在计算( )
我国是最早认识负数,并进行相关运算的国家.在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算3+(-4)的过程.按照这种方法,图2表示的过程应是在计算( )| A、(-5)+(-2) |
| B、(-5)+2 |
| C、5+(-2) |
| D、5+2 |
 如图,△ABC内接于⊙O,AB为⊙O的直径,∠ACB的平分线CD交⊙O于点D,过点D作⊙O的切线PD,交CA的延长线于点F,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
如图,△ABC内接于⊙O,AB为⊙O的直径,∠ACB的平分线CD交⊙O于点D,过点D作⊙O的切线PD,交CA的延长线于点F,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.