题目内容
如果将抛物线y=-2x2平移,使顶点移到点P(-3,1)的位置,那么所得新抛物线的表达式是 .
考点:二次函数图象与几何变换
专题:几何变换
分析:由于抛物线平移前后二次项系数不变,然后根据顶点式写出新抛物线解析式.
解答:解:抛物线y=-2x2平移,使顶点移到点P(-3,1)的位置,所得新抛物线的表达式为y=-2(x+3)2+1.
故答案为y=-2(x+3)2+1.
故答案为y=-2(x+3)2+1.
点评:本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
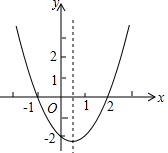 二次函数y=ax2+bx+c的图象如图所示,则下列结论中错误的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列结论中错误的是( )| A、函数有最小值 | ||
| B、当-1<x<2时,y>0 | ||
| C、a+b+c<0 | ||
D、当x<
|
抛物线y=-x2不具有的性质是( )
| A、开口向上 |
| B、对称轴是y轴 |
| C、在对称轴的左侧,y随x的增大而增大 |
| D、最高点是原点 |
为了估计湖中有多少条鱼.先从湖中捕捉50条鱼作记号,然后放回湖里,经过段时间,等带记号的鱼完全混于鱼群中之后再捕捞,第二次捕鱼共20条,有10条做了记号,则估计湖里有鱼( )
| A、400条 | B、500条 |
| C、800条 | D、100条 |
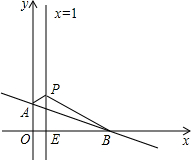 如图,平面直角坐标系中,直线AB:y=-
如图,平面直角坐标系中,直线AB:y=-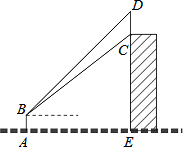 如图,某幢大楼的外墙边上竖直安装着一根旗杆CD,小明在离旗杆下方大楼底部E点24米的点A处放置一台测角仪,测角仪的高度AB为1.5米,并在点B处测得旗杆下端C的仰角为40°,上端D的仰角为45°,求旗杆CD的长度;(结果精确到0.1米,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
如图,某幢大楼的外墙边上竖直安装着一根旗杆CD,小明在离旗杆下方大楼底部E点24米的点A处放置一台测角仪,测角仪的高度AB为1.5米,并在点B处测得旗杆下端C的仰角为40°,上端D的仰角为45°,求旗杆CD的长度;(结果精确到0.1米,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)