题目内容
13.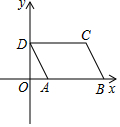 如图,在平面直角坐标系中,已知A(1,0),B(5,0),现同时将点A,B分别向左平移1个单位长度,再向上平移m个单位长度,得到A,B的对应点D,C,连接AD,BC,CD.
如图,在平面直角坐标系中,已知A(1,0),B(5,0),现同时将点A,B分别向左平移1个单位长度,再向上平移m个单位长度,得到A,B的对应点D,C,连接AD,BC,CD.(1)请用含m的式子表示三角形DAB的面积;
(2)在(1)条件下,当m=2时,在x轴上存在点F,使得三角形DFA的面积是三角形DAB面积的$\frac{1}{2}$,请求出点F的坐标;
(3)在(2)结论下,连接FC,FD,请直接写出∠DFC与∠BCF,∠ADF的数量关系.
分析 (1)根据A(1,0),B(5,0),可得AO=1,AB=4,根据当点A向左平移1个单位长度时与O重合,再向上平移m个单位长度得到D,可得OD=m,进而得出S△ABD=$\frac{1}{2}$AB×OD=2m;
(2)设F(n,0),则由A(1,0),可得AF=|n-1|,进而得到S△ADF=$\frac{1}{2}$AF×OD=|n-1|,再根据三角形DFA的面积是三角形DAB面积的$\frac{1}{2}$,可得方程|n-1|=$\frac{1}{2}$×4,求得n=3或-1,进而得出点F的坐标;
(3)分两种情况:①当点F的坐标为(3,0)时,连接FC,FD,过F作FG∥AD,②当点F的坐标为(-1,0)时,连接FC,FD,过F作FG∥AD,分别根据平行线的性质以及角的和差关系进行计算求解.
解答 解:(1)由平移得,AD∥BC,AD=BC,
∵A(1,0),B(5,0),
∴AO=1,AB=4,
∴当点A向左平移1个单位长度时与O重合,再向上平移m个单位长度得到D,即OD=m,
∴S△ABD=$\frac{1}{2}$AB×OD=$\frac{1}{2}$×4×m=2m;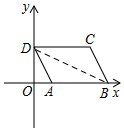
(2)当m=2时,S△ABD=2m=4,
设F(n,0),则由A(1,0),可得AF=|n-1|,
∴S△ADF=$\frac{1}{2}$AF×OD=$\frac{1}{2}$|n-1|×2=|n-1|,
又∵三角形DFA的面积是三角形DAB面积的$\frac{1}{2}$,
∴|n-1|=$\frac{1}{2}$×4,
解得n=3或-1,
∴点F的坐标为(-1,0)或(3,0);
(3)∠DFC=∠ADF+∠BCF或∠DFC=∠BCF-∠ADF.
分两种情况:
①如图所示,当点F的坐标为(3,0)时,连接FC,FD,过F作FG∥AD,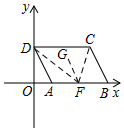
∵AD∥BC,
∴FG∥BC,
∴∠ADF=∠GFD,∠BCF=∠GFC,
∴∠DFC=∠GFD+∠GFC=∠ADF+∠BCF;
②如图所示,当点F的坐标为(-1,0)时,连接FC,FD,过F作FG∥AD,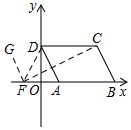
∵AD∥BC,
∴FG∥BC,
∴∠ADF=∠GFD,∠BCF=∠GFC,
∴∠DFC=∠GFC-∠GFD=∠BCF-∠ADF.
点评 本题主要考查了平移的性质,平行线的性质以及三角形面积公式的运用,解题时注意根据点F的不同位置,进行分类讨论.解决问题的关键是作辅助线构造内错角,运用平行线的性质进行计算.

| A. |  | B. |  | C. |  | D. |  |
| A. | 5,8 | B. | 8,8 | C. | 5,11 | D. | 11,11 |
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 8$\sqrt{3}$ |
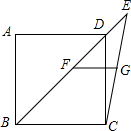 如图,已知在正方形ABCD中,连接BD并延长至点E,连接CE,F、G分别为BE,CE的中点,连接FG.若AB=6,则FG的长度为( )
如图,已知在正方形ABCD中,连接BD并延长至点E,连接CE,F、G分别为BE,CE的中点,连接FG.若AB=6,则FG的长度为( )