题目内容
18．
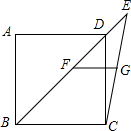如图，已知在正方形ABCD中，连接BD并延长至点E，连接CE，F、G分别为BE，CE的中点，连接FG．若AB=6，则FG的长度为（ ）| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
分析 根据三角形中位线定理可知FG=$\frac{1}{2}$BC，由此即可解决问题．
解答 解：∵四边形ABCD是正方形，
∴AB=BC=6，
∵F、G分别为BE，CE的中点，
∴FG=$\frac{1}{2}$BC=3，
故选A．
点评 本题考查正方形的性质、三角形的中位线定理等知识，几天倒计时灵活运用所学知识解决问题，属于中考常考题型．
练习册系列答案
相关题目
9．不等式组$\left\{\begin{array}{l}{x+2≥0}\\{\frac{x}{2}-1＜-\frac{1}{2}}\end{array}\right.$的解集在数轴上表示为（ ）
| A． |  | B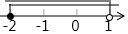． |  | C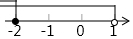． |  | D． |  |
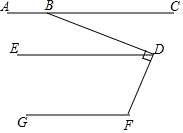如图，已知AC∥ED，ED∥GF，∠BDF=90°．
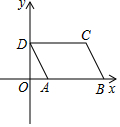如图，在平面直角坐标系中，已知A（1，0），B（5，0），现同时将点A，B分别向左平移1个单位长度，再向上平移m个单位长度，得到A，B的对应点D，C，连接AD，BC，CD．
3．在-1，$\frac{1}{3}$，$\sqrt{2}$，0.7中，无理数是（ ）
| A． | -1 | B． | $\frac{1}{3}$ | C． | $\sqrt{2}$ | D． | 0.7 |
如图，矩形ABCD的两条对角线相交于点O，∠AOD=60°，AD=1，则AC的长是2．
7．
如图，△ABC的角平分线BE，CF相交于点O，且∠FOE=121°，则∠A的度数是（ ）
如图，△ABC的角平分线BE，CF相交于点O，且∠FOE=121°，则∠A的度数是（ ）| A． | 52° | B． | 62° | C． | 64° | D． | 72° |