题目内容
2.先化简,再求值:(m+2-$\frac{5}{m-2}$)•$\frac{2m-4}{3-m}$,其中m=-$\frac{1}{2}$.分析 此题的运算顺序:先括号里,经过通分,再约分化为最简,最后代值计算.
解答 解:(m+2-$\frac{5}{m-2}$)•$\frac{2m-4}{3-m}$,
=$\frac{{m}^{2}-4-5}{m-2}$•$\frac{2(m-2)}{3-m}$,
=-$\frac{(m+3)(m-3)}{m-2}$•$\frac{2(m-2)}{m-3}$,
=-2(m+3).
把m=-$\frac{1}{2}$代入,得
原式=-2×(-$\frac{1}{2}$+3)=-5.
点评 本题考查了分式的化简求值.分式混合运算要注意先去括号;分子、分母能因式分解的先因式分解.

练习册系列答案
相关题目
12.函数y=$\frac{1}{x+1}$中,自变量x的取值范围是( )
| A. | x≠-1 | B. | x≠1 | C. | x>-1 | D. | x≥-1 |
17.一组数据:1、2、2、3,若添加一个数据2,则发生变化的统计量是( )
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
7. 如图,△ABC的角平分线BE,CF相交于点O,且∠FOE=121°,则∠A的度数是( )
如图,△ABC的角平分线BE,CF相交于点O,且∠FOE=121°,则∠A的度数是( )
 如图,△ABC的角平分线BE,CF相交于点O,且∠FOE=121°,则∠A的度数是( )
如图,△ABC的角平分线BE,CF相交于点O,且∠FOE=121°,则∠A的度数是( )| A. | 52° | B. | 62° | C. | 64° | D. | 72° |
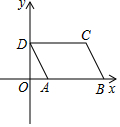 如图,在平面直角坐标系中,已知A(1,0),B(5,0),现同时将点A,B分别向左平移1个单位长度,再向上平移m个单位长度,得到A,B的对应点D,C,连接AD,BC,CD.
如图,在平面直角坐标系中,已知A(1,0),B(5,0),现同时将点A,B分别向左平移1个单位长度,再向上平移m个单位长度,得到A,B的对应点D,C,连接AD,BC,CD. 如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=1,则AC的长是2.
如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=1,则AC的长是2.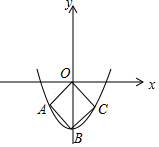 如图,抛物线y=$\frac{1}{2}$x2+c的顶点B在y轴的负半轴上,正方形OABC的两个顶点A,C在抛物线上,则c的值是-4.
如图,抛物线y=$\frac{1}{2}$x2+c的顶点B在y轴的负半轴上,正方形OABC的两个顶点A,C在抛物线上,则c的值是-4.