题目内容
3.(1)解方程组:$\left\{\begin{array}{l}{x-y=4}\\{2x+y=5}\end{array}\right.$(2)解不等式:$\frac{x}{3}$>1-$\frac{x-2}{2}$.
分析 (1)用加减消元法求出方程组的解.
(2)根据一元一次不等式的解法,去分母,去括号,移项,合并,系数化为1即可得解.
解答 解:(1)$\left\{\begin{array}{l}{x-y=4①}\\{2x+y=5②}\end{array}\right.$,
①+②得:3x=9,
x=3,
代入①得:3-y=4,
y=-1.
则原方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$.
(2)去分母得,2x>6-3(x-2),
去括号得,2x>6-3x+6,
移项、合并得,5x>12,
系数化为1得,x>$\frac{12}{5}$.
点评 此题主要考查了二元一次方程组合解一元一次不等式,掌握解一元一次不等式的一般步骤和解方程组的方法上解题得关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
18.我国对“一带一路”沿线国家不断加大投资,目前已为有关国家创造了近1100000000美元税收,其中1100000000用科学记数法表示应为( )
| A. | 0.11×108 | B. | 1.1×109 | C. | 1.1×1010 | D. | 11×108 |
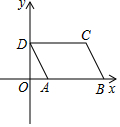 如图,在平面直角坐标系中,已知A(1,0),B(5,0),现同时将点A,B分别向左平移1个单位长度,再向上平移m个单位长度,得到A,B的对应点D,C,连接AD,BC,CD.
如图,在平面直角坐标系中,已知A(1,0),B(5,0),现同时将点A,B分别向左平移1个单位长度,再向上平移m个单位长度,得到A,B的对应点D,C,连接AD,BC,CD.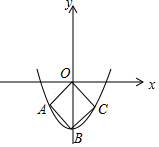 如图,抛物线y=$\frac{1}{2}$x2+c的顶点B在y轴的负半轴上,正方形OABC的两个顶点A,C在抛物线上,则c的值是-4.
如图,抛物线y=$\frac{1}{2}$x2+c的顶点B在y轴的负半轴上,正方形OABC的两个顶点A,C在抛物线上,则c的值是-4.