题目内容
5.已知等边三角形的边长为4,则它的高为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 8$\sqrt{3}$ |
分析 根据等边三角形三线合一的性质可以求得高线AD的长度.
解答  解:如图,∵等边三角形三线合一,
解:如图,∵等边三角形三线合一,
∴D为BC的中点,BD=DC=2,
在Rt△ABD中,AB=4,BD=2,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=2$\sqrt{3}$,
故选B.
点评 本题考查了勾股定理在直角三角形中的运用,考查了三角形面积的计算,考查了等边三角形各边长相等的性质,本题中根据勾股定理即可AD的长度是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.一组数据:1、2、2、3,若添加一个数据2,则发生变化的统计量是( )
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
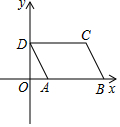 如图,在平面直角坐标系中,已知A(1,0),B(5,0),现同时将点A,B分别向左平移1个单位长度,再向上平移m个单位长度,得到A,B的对应点D,C,连接AD,BC,CD.
如图,在平面直角坐标系中,已知A(1,0),B(5,0),现同时将点A,B分别向左平移1个单位长度,再向上平移m个单位长度,得到A,B的对应点D,C,连接AD,BC,CD. 如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=1,则AC的长是2.
如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=1,则AC的长是2.