题目内容
已知抛物线过点A（-3，8）及B（5，8），则它的对称轴为直线 ．
考点：二次函数的性质
专题：
分析：点A（-3，8）及B（5，8）的纵坐标相同，这两点一定关于对称轴对称，那么利用两点的横坐标可求对称轴．
解答：解：∵点A（-3，8）及B（5，8）的纵坐标相同，
∴这两点一定关于对称轴对称，
∴对称轴是：x=
=1，
故答案为：x=1．
∴这两点一定关于对称轴对称，
∴对称轴是：x=
| -3+5 |
| 2 |
故答案为：x=1．
点评：本题主要考查了抛物线的对称性，图象上的两点的纵坐标相同，则这两点一定关于对称轴对称．
练习册系列答案
相关题目
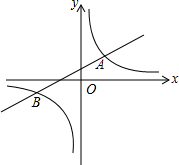如图，一次函数y1=k1+2与反比例函数y2=| k2 |
| x |
| A、x＜-8或0＜x＜4 |
| B、x＞4或-8＜x＜0 |
| C、-8＜x＜4 |
| D、x＜-8或x＞4 |
抛物线y=x2+bx+c向左平移2个单位，再向下平移3个单位后得到抛物线y=x2-2x+1，则（ ）
| A、b=-6，c=12 |
| B、b=-8，c=-14 |
| C、b=6，c=12 |
| D、b=-8，c=14 |
