题目内容
如图,在下面由火柴棒拼出的一系列的图形中,第n个图形由n个正方形组成.第10个图形中,火柴棒的根数是 ;第 个图形时所用的火柴数量是2014根.


考点:规律型:图形的变化类
专题:
分析:拼1个正方形中火柴棒的根数是4,拼2个正方形中火柴棒的根数是(4×2-1),拼3个正方形中火柴棒的根数是(4×3-2),拼4个正方形中火柴棒的根数是(4×4-3)…拼n个正方形中火柴棒的根数是[4n-(n-1)].
解答:解:(1)第1个图形中火柴棒的根数是:4
第2个图形中火柴棒的根数是:4×2-1=7
第3个图形中火柴棒的根数是:4×3-2=10
第4个图形中火柴棒的根数是:4×4-3=13.
…
第10个图形中火柴棒的根数是4×10-9=31根;
(2)第n个图形中火柴棒的根数是:4n-(n-1)=3n+1.
当3n+1=2014时,解得:n=671
故答案为:31,671.
第2个图形中火柴棒的根数是:4×2-1=7
第3个图形中火柴棒的根数是:4×3-2=10
第4个图形中火柴棒的根数是:4×4-3=13.
…
第10个图形中火柴棒的根数是4×10-9=31根;
(2)第n个图形中火柴棒的根数是:4n-(n-1)=3n+1.
当3n+1=2014时,解得:n=671
故答案为:31,671.
点评:本题考查了图形的变化类问题,注意结合图形,发现蕴含的规律,找出解决问题的途径.注意由特殊到一般的分析方法.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
将正偶数按下表排成5列若干行,根据上述规律,2012应在( )


| A、第251行,第4列 |
| B、第251行,第5列 |
| C、第252行,第3列 |
| D、第252行,第4列 |
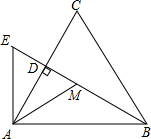 如图,已知△ABC是等边三角形,BD是AC上的高线.作AE⊥AB于点A,交BD的延长线于点E.取BE的中点M,连结AM.
如图,已知△ABC是等边三角形,BD是AC上的高线.作AE⊥AB于点A,交BD的延长线于点E.取BE的中点M,连结AM.