题目内容
6.为体现社会对教师的尊重,2016年教师节这一天上午,出租车司机小李在东西方向的友谊路上免费接送老师.以出发点为起点,如果规定向东为正,向西为负,出租车的行程如下(单位:千米):+15,-4,+13,-10,-12,+3,-13,-17.(1)请问把最后一名老师送到目的地时,小李位于出发地的哪个方向?距离出发地多远?
(2)在接送老师的过程中,出租车行驶到最远处时离出发地有多远?
(3)若出租车每行驶100千米耗油10升,这天上午出租车共耗油多少升?
分析 (1)本题需先根据正数和负数的表示方法和本题所给的已知条件,分别计算出小李位于出发地地点的哪边和距离出发地多远即可;
(2)计算出每次接送老师离出发点的距离,得出离出发点最远处时离出发地有多远;
(3)本题需先根据出租车耗油量和出租车走的路程列出式子,得出结果即可求出这天上午出租车共耗油量.
解答 解:(1)15-4+13-10-12+3-13-17=-25(km).
答:位于出发地西边,距离出发地25千米;
(2)15-4=11,
11+13=24,
24-10=14,
14-12=2,
2+3=5,
5-13=-8,
-8-17=25.
答:出租车行驶到最远处时离出发地有25千米远;
(3)(15+4+13+10+12+3+13+17)÷100×10
=87÷100×10
=8.7(升).
答:这天上午出租车共耗油8.7升.
点评 此题考查的知识点是正数和负数,解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.一般情况下具有相反意义的量才是一对具有相反意义的量.

练习册系列答案
相关题目
18.下列角度中,不可能是多边形内角和的是( )
| A. | 540° | B. | 630° | C. | 720° | D. | 900° |
19.若多项式x2+px+12可以因式分解为(x+m)(x+n)的形式,且p、m、n均为整数,则满足条件的整数p共有( )
| A. | 2个 | B. | 4个 | C. | 6个 | D. | 8个 |
16.已知关于x的一元二次方程2x2-3kx+4的一个根是1,则k等于( )
| A. | 2 | B. | -2 | C. | 0 | D. | 1 |
18.点A、C为半径是3的圆周上两点,点B为$\widehat{AC}$的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为( )
| A. | $\sqrt{5}$或2$\sqrt{2}$ | B. | $\sqrt{5}$或2$\sqrt{3}$ | C. | $\sqrt{6}$或2$\sqrt{2}$ | D. | $\sqrt{6}$或2$\sqrt{3}$ |
16.某厂生产一种工具,据市场调查,若按每个工具280元销售时,每月可销售300个,若销售单价每降低1元,每月可多售出2个,据统计,每个工具的固定成本Q(元)与月销售y(个)满足如下关系:
(1)写出月产销量y(个)与销售单价x(元)之间的函数关系式;
(2)求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?
| 月销量y(个) | 100 | 160 | 240 | 320 |
| 每个工具的固定成本Q(元) | 96 | 60 | 40 | 30 |
(2)求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?
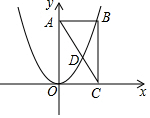 如图,抛物线y=ax2经过矩形OABC的顶点B,交对角线AC于点D.则$\frac{AD}{AC}$的值为$\frac{\sqrt{5}-1}{2}$.
如图,抛物线y=ax2经过矩形OABC的顶点B,交对角线AC于点D.则$\frac{AD}{AC}$的值为$\frac{\sqrt{5}-1}{2}$.