题目内容
1.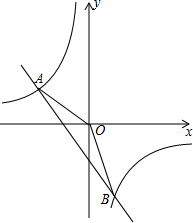 如图,已知反比例函数y1=$\frac{m}{x}$的图象与一次函数y2=kx+b的图象交于两点A(-2,1),B(a,-2).
如图,已知反比例函数y1=$\frac{m}{x}$的图象与一次函数y2=kx+b的图象交于两点A(-2,1),B(a,-2).(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)试根据图象写出不等式$\frac{m}{x}$>kx+b的解集.
分析 (1)先把A点坐标代入代入y1=$\frac{m}{x}$求出m确定反比例函数解析式为y1=-$\frac{2}{x}$;再把B(a,2)代入y1=-$\frac{2}{x}$求出a,确定B点坐标为(1,-2),然后利用待定系数法确定一次函数解析式;
(2)求得直线与y轴的交点,然后根据S△AOB=S△AOC+S△BOC即可求得;
(3)观察函数图象,当-2<x<0或x>1时,反比例函数图象都在一次函数图象上方,据此即可求解.
解答 解:(1)把A(-2,1)代入y1=$\frac{m}{x}$得m=1×(-2)=-2,
所以反比例函数解析式为y1=-$\frac{2}{x}$;
把B(a,-2)代入y1=-$\frac{2}{x}$得2a=2,解得a=1,
所以B点坐标为(1,-2),
把A(1,-2)和B(-2,1)代入y2=kx+b得$\left\{\begin{array}{l}{k+b=-2}\\{-2k+b=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=-1}\end{array}\right.$,
所以一次函数解析式为y1=-x-1;
(2)设直线与y轴的交点为C,
∵一次函数解析式为y1=-x-1;
∴C(0,-1),
∴S△AOB=S△AOC+S△BOC=$\frac{1}{2}$×1×2+$\frac{1}{2}×1$×1=$\frac{3}{2}$.
(3)不等式$\frac{m}{x}$>kx+b的解集为-2<x<0或x>1.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列命题中是假命题的是( )
| A. | 垂直于弦的直径平分弦 | |
| B. | 若a>b,c>0,则ac>bc | |
| C. | 反比例函数y=$\frac{k}{x}$,当k>0时,y随x的增大而减少 | |
| D. | 对角线互相平分且垂直的四边形是菱形 |
16.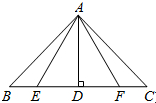 如图所示,△ABC中,AB=AC,BE=CF,AD⊥BC,则图中共有全等三角形( )
如图所示,△ABC中,AB=AC,BE=CF,AD⊥BC,则图中共有全等三角形( )
 如图所示,△ABC中,AB=AC,BE=CF,AD⊥BC,则图中共有全等三角形( )
如图所示,△ABC中,AB=AC,BE=CF,AD⊥BC,则图中共有全等三角形( )| A. | 4对 | B. | 3对 | C. | 2对 | D. | 1对 |
 正整数如图的规则排列,则:
正整数如图的规则排列,则: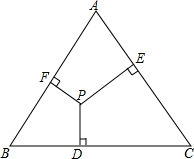 有一块等边三角形的空地,小明和小亮想在这块空地上找到一点,使得这一点到三边的距离之和最短,他们做了几次实验,发现无论三角形内的哪一点到三边的距离之和都是相等的.于是他们编了一道几何题:如图,已知点P为正△ABC内一点,点P到BC,CA,AB的距离分别为PD,PE,PF,试说明PD+PE+PF总是一个定值.这个定值与什么有关?你发现这个事实了吗?你能解出他们编的数学问题吗?
有一块等边三角形的空地,小明和小亮想在这块空地上找到一点,使得这一点到三边的距离之和最短,他们做了几次实验,发现无论三角形内的哪一点到三边的距离之和都是相等的.于是他们编了一道几何题:如图,已知点P为正△ABC内一点,点P到BC,CA,AB的距离分别为PD,PE,PF,试说明PD+PE+PF总是一个定值.这个定值与什么有关?你发现这个事实了吗?你能解出他们编的数学问题吗?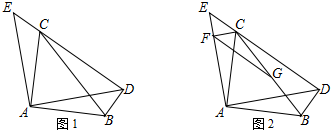
 如图,一块草地的中间有一条宽度不变的弯路,AC∥BD,CE∥EF,请给出一种方案,把道路改直,且草地的种植面积保持不变.
如图,一块草地的中间有一条宽度不变的弯路,AC∥BD,CE∥EF,请给出一种方案,把道路改直,且草地的种植面积保持不变.