Question

3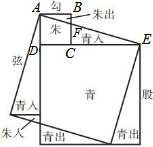． 魏朝时期，刘徽利用下图通过“以盈补虚，出入相补”的方法，即“勾自乘为朱方，股自乘为青方，令出入相补，各从其类”证明了勾股定理．若图中BF=1，CF=2，则AE的长为3$\sqrt{10}$．

Answer 1

分析 由BF+CF求出BC的长，即为正方形ABCD的边长，由AB与CE平行，得比例求出CE的长，由DC+CE求出DE的长，在直角三角形ADE中，利用勾股定理求出AE的长即可．

解答 解：∵BF=1，CF=2，
∴BC=BF+CF=1+2=3，
∵AB∥EC，
∴$\frac{AB}{CE}$=$\frac{BF}{CF}$，即$\frac{3}{CE}$=$\frac{1}{2}$，
解得：CE=6，
在Rt△ADE中，AD=3，DE=DC+CE=3+6=9，
根据勾股定理得：AE=$\sqrt{{3}^{2}+{9}^{2}}$=3$\sqrt{10}$，
故答案为：3$\sqrt{10}$

点评 此题考查了勾股定理的证明，以及相似三角形的判定与性质，熟练掌握勾股定理是解本题的关键．