题目内容
13.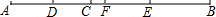 如图,已知,C为线段AB上一点,D为AC的中点,E为BC的中点,F为DE的中点
如图,已知,C为线段AB上一点,D为AC的中点,E为BC的中点,F为DE的中点(1)如图1,若AC=4,BC=6,求CF的长;
(2)若AB=16CF,求$\frac{AC}{CB}$的值;
(3)若AC>BC,AC-BC=a,取DC的中点G,CE的中点H,GH的中点P,求CP的长(用含a的式子表示).
分析 (1)由D为AC的中点,E为BC的中点得到DC=$\frac{1}{2}$AC=2,CE=$\frac{1}{2}$BC=3,则可计算出DE=5,再利用F为DE的中点得到DF=$\frac{1}{2}$DE=$\frac{5}{2}$,然后利用CF=DF-DC求解;
(2)设AC=x,BC=y,易得DE=DC+CE=$\frac{1}{2}$(x+y),再计算出DF=$\frac{1}{2}$DE=$\frac{1}{4}$(x+y),所以CF=DF-DC=$\frac{1}{4}$(y-x),接着利用AB=16CF得到x+y=16•$\frac{1}{4}$(y-x),化简后有5x=3y,然后利用比例性质即可得到$\frac{AC}{CB}$的值;
(3)如图,设AC=x,BC=y,即x-y=a,利用线段中点定义得到DC=$\frac{1}{2}$x,CE=$\frac{1}{2}$y,则HC=$\frac{1}{4}$x,CH=$\frac{1}{4}$y,所以GH=$\frac{1}{4}$(x+y),再利用GH的中点为P得到GP=$\frac{1}{2}$GH=$\frac{1}{8}$(x+y),于是可计算出PC=GC-GP=$\frac{1}{8}$(x-y),即有CP=$\frac{1}{8}$a.
解答 解:(1)∵D为AC的中点,E为BC的中点,
∴DC=$\frac{1}{2}$AC=2,CE=$\frac{1}{2}$BC=3,
∴DE=DC+CE=2+3=5,
∵F为DE的中点,
∴DF=$\frac{1}{2}$DE=$\frac{5}{2}$,
∴CF=DF-DC=$\frac{5}{2}$-2=$\frac{1}{2}$;
(2)设AC=x,BC=y,则DC=$\frac{1}{2}$AC=$\frac{1}{2}$x,CE=$\frac{1}{2}$BC=$\frac{1}{2}$y,
∴DE=DC+CE=$\frac{1}{2}$(x+y),
∵F为DE的中点,
∴DF=$\frac{1}{2}$DE=$\frac{1}{4}$(x+y),
∴CF=DF-DC=$\frac{1}{4}$(x+y)-$\frac{1}{2}$x=$\frac{1}{4}$(y-x);
∵AB=16CF,
∴x+y=16•$\frac{1}{4}$(y-x),
∴5x=3y,
∴$\frac{x}{y}$=$\frac{3}{5}$,
即$\frac{AC}{BC}$的值为$\frac{3}{5}$;
(3)如图,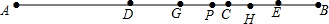
设AC=x,BC=y,即x-y=a,则DC=$\frac{1}{2}$AC=$\frac{1}{2}$x,CE=$\frac{1}{2}$BC=$\frac{1}{2}$y,
∵DC的中点为G,CE的中点为H,
∴GC=$\frac{1}{2}$CD=$\frac{1}{4}$x,CH=$\frac{1}{2}$CE=$\frac{1}{4}$y,
∴GH=$\frac{1}{4}$(x+y),
∵GH的中点为P,
∴GP=$\frac{1}{2}$GH=$\frac{1}{8}$(x+y),
∴PC=GC-GP=$\frac{1}{4}$x-$\frac{1}{8}$(x+y)=$\frac{1}{8}$(x-y),
∴PC=$\frac{1}{8}$a.
点评 本题考查了两点间的距离:连接两点间的线段的长度叫两点间的距离.理清线段之间的关系是解决本题的关键.

 科学实验活动册系列答案
科学实验活动册系列答案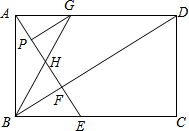 如图,在矩形ABCD中,AE⊥BD交BC于E,垂足为F,BG平分∠ABD交AE于H,GP∥BD交AE于P,下列结论:
如图,在矩形ABCD中,AE⊥BD交BC于E,垂足为F,BG平分∠ABD交AE于H,GP∥BD交AE于P,下列结论: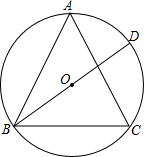 等边三角形ABC的顶点都在圆O上,BD为直径,则∠BDC=60°,∠ACD=30°,若CD=6cm,则△ABC的面积等于27$\sqrt{3}$cm2.
等边三角形ABC的顶点都在圆O上,BD为直径,则∠BDC=60°,∠ACD=30°,若CD=6cm,则△ABC的面积等于27$\sqrt{3}$cm2.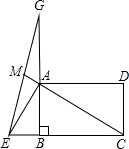 如图,矩形ABCD中,AB=3,AD=3$\sqrt{3}$,点E在CB的延长线上,且BE=$\sqrt{3}$,连结AE,G是BA延长线上一点,连结EG,交CA的延长线于M,将△AEG绕点A逆时针旋转60°得到△AE′G′(点E的对应点为E′,点G的对应点为G′).若△EGG′的面积为6$\sqrt{3}$,则CM的长为7.
如图,矩形ABCD中,AB=3,AD=3$\sqrt{3}$,点E在CB的延长线上,且BE=$\sqrt{3}$,连结AE,G是BA延长线上一点,连结EG,交CA的延长线于M,将△AEG绕点A逆时针旋转60°得到△AE′G′(点E的对应点为E′,点G的对应点为G′).若△EGG′的面积为6$\sqrt{3}$,则CM的长为7.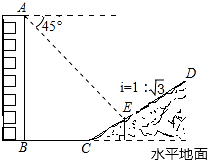 如图,一楼房AB后有一假山,其坡度为i=1:$\sqrt{3}$,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=26米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°.(注:坡度i是指坡面的铅直高度与水平宽度的比)
如图,一楼房AB后有一假山,其坡度为i=1:$\sqrt{3}$,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=26米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°.(注:坡度i是指坡面的铅直高度与水平宽度的比)