题目内容
18.当1<x<3时,化简$\sqrt{(x-3)^{2}}$+$\sqrt{(1-x)^{2}}$=2.分析 当1<x<3时利用二次根式的性质化简即可.
解答 解:因为1<x<3,
所以可得:$\sqrt{(x-3)^{2}}$+$\sqrt{(1-x)^{2}}$=3-x+x-1=2,
故答案为:2.
点评 此题考查二次根式问题,关键是根据二次根式的性质化简.

练习册系列答案
相关题目
9.a、b、c是△ABC的∠A、∠B、∠C的对边,且a:b:c=1:$\sqrt{2}$:$\sqrt{3}$,则cosB的值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
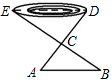 如图,为了测量一个池塘的宽DE,在岸边找一个点C,测得CD=15m,在DC的延长线上找一点A,使AC=10m,过A作AB∥DE交EC的延长线于点B,测得AB=16m,求池塘的宽DE.
如图,为了测量一个池塘的宽DE,在岸边找一个点C,测得CD=15m,在DC的延长线上找一点A,使AC=10m,过A作AB∥DE交EC的延长线于点B,测得AB=16m,求池塘的宽DE.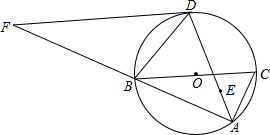 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D,BC是⊙O的直径,⊙O的切线FD与AB的延长线交于点F.
如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D,BC是⊙O的直径,⊙O的切线FD与AB的延长线交于点F.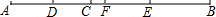 如图,已知,C为线段AB上一点,D为AC的中点,E为BC的中点,F为DE的中点
如图,已知,C为线段AB上一点,D为AC的中点,E为BC的中点,F为DE的中点
 如图,在△ABC中,∠ABC=100°,∠ACB的平分线交AB边于E,在AC边上有一点D满足∠CBD=20°,连结DE,求∠CED的度数.
如图,在△ABC中,∠ABC=100°,∠ACB的平分线交AB边于E,在AC边上有一点D满足∠CBD=20°,连结DE,求∠CED的度数.