题目内容
18. 如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点灯A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则点C′到BC的距离为$\frac{1}{2}\sqrt{2}$.
如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点灯A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则点C′到BC的距离为$\frac{1}{2}\sqrt{2}$.
分析 连接BB′,过C'作C'D⊥BC于D,作C'E⊥AC于E,先判定△ABB′是等边三角形,△AB′C′是等腰直角三角形,进而得到∠C'AE=60°,∠AC'E=30°,再根据AE的长即可得到CE,据此可得点C′到BC的距离.
解答  解:如图,连接BB′,过C'作C'D⊥BC于D,作C'E⊥AC于E,
解:如图,连接BB′,过C'作C'D⊥BC于D,作C'E⊥AC于E,
∵△ABC绕点A顺时针方向旋转60°得到△AB′C′,
∴AB=AB′,∠BAB′=60°,
∴△ABB′是等边三角形,
∴∠BAB'=60°,
∵△ABC中,∠C=90°,AC=BC,
∴△ABC是等腰直角三角形,
∴△AB′C′是等腰直角三角形,
∴∠B'AC'=45°,
∴∠BAC'=60°-45°=15°,
∴∠C'AE=60°,∠AC'E=30°,
由旋转可得,AC'=AC=$\sqrt{2}$,
∴Rt△AC'E中,AE=$\frac{1}{2}$AC'=$\frac{1}{2}\sqrt{2}$,
∴CE=AC-AE=$\sqrt{2}$-$\frac{1}{2}\sqrt{2}$=$\frac{1}{2}\sqrt{2}$,
又∵∠C=∠CDC'=∠CEC'=90°,
∴矩形DCEC'中,C'D=EC=$\frac{1}{2}\sqrt{2}$,
故答案为:$\frac{1}{2}\sqrt{2}$.
点评 本题主要考查了旋转的性质,等腰直角三角形的性质以及等边三角形的判定与性质的综合应用,解决问题的关键是作辅助线构造等边三角形以及含30°角的直角三角形.

练习册系列答案
相关题目
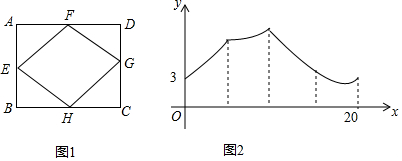
6.如图1,已知点E,F,G,H是矩形ABCD各边的中点,AB=6,BC=8,动点M从点E出发,沿E→F→G→H→E匀速运动,设点M运动的路程x,点M到矩形的某一个顶点的距离为y,如果表示y关于x函数关系的图象如图2所示,那么这个顶点是矩形的( )

| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
3.二次函数y=2x2+4x-3的图象的对称轴为( )
| A. | 直线x=2 | B. | 直线x=4 | C. | 直线x=-3 | D. | 直线x=-1 |
 如图,两条直线分别被三条平行直线l1,l2,l3所截,若AB=3,BC=6,DE=2,则DF的长为( )
如图,两条直线分别被三条平行直线l1,l2,l3所截,若AB=3,BC=6,DE=2,则DF的长为( )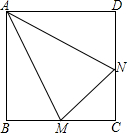 如图,M、N分别是正方形ABCD的边BC、CD上的点,已知:∠MAN=30°,AM=AN,△AMN的面积为1.
如图,M、N分别是正方形ABCD的边BC、CD上的点,已知:∠MAN=30°,AM=AN,△AMN的面积为1.