题目内容
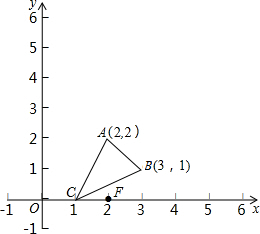 如图,△ABC的三个顶点坐标分别为A(2,2),B(3,1),C(1,0),试将△ABC放大,使放大后的△DEF与△ABC对应边之比为2:1,并指出其对应边AB与DE有何位置关系?并说明理由.
如图,△ABC的三个顶点坐标分别为A(2,2),B(3,1),C(1,0),试将△ABC放大,使放大后的△DEF与△ABC对应边之比为2:1,并指出其对应边AB与DE有何位置关系?并说明理由.考点:作图-位似变换
专题:
分析:由△ABC的三个顶点坐标分别为A(2,2),B(3,1),C(1,0),试将△ABC放大,使放大后的△DEF与△ABC对应边之比为2:1,根据位似图形的性质,即可作出图形,然后由位似的性质,即可证得AB∥DE.
解答: 解:AB∥DE.
解:AB∥DE.
理由:连接OD,OE,
∵△DEF与△ABC位似,O是位似中心,位似比为2:1,
∴点A在OD上,点B在OE上,且OA:OD=OB:OE=1:2,
∴AB∥DE.
 解:AB∥DE.
解:AB∥DE.理由:连接OD,OE,
∵△DEF与△ABC位似,O是位似中心,位似比为2:1,
∴点A在OD上,点B在OE上,且OA:OD=OB:OE=1:2,
∴AB∥DE.
点评:此题考查了位似图形的性质与位似变换.此题难度不大,注意掌握位似图形的性质是解此题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
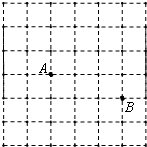 如图是一个6×6的正方形网格,每个小正方形的顶点都是格点,等腰△ABC的顶点都是图中的格点,其中点A、点B的位置如图所示,则点C可能的位置共有( )
如图是一个6×6的正方形网格,每个小正方形的顶点都是格点,等腰△ABC的顶点都是图中的格点,其中点A、点B的位置如图所示,则点C可能的位置共有( )| A、12个 | B、11个 |
| C、10个 | D、9个 |
半径为1的圆形纸片按如下图所示的方法黏合起来,则1000张纸黏合后的长度是( )


| A、999 | B、1000 |
| C、1001 | D、1999 |
 已知a,b,c在数轴上的对应点如图所示,化简:
已知a,b,c在数轴上的对应点如图所示,化简: 如图,平行四边形ABCD中,对角线AC、BD交于O,E是AO中点,BE的延长线与BD的平行线AF交于点F.
如图,平行四边形ABCD中,对角线AC、BD交于O,E是AO中点,BE的延长线与BD的平行线AF交于点F.
 如图,矩形ABCD为台球桌面,AD=280cm,AB=140cm,球目前在E点位置,AE=35cm,如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
如图,矩形ABCD为台球桌面,AD=280cm,AB=140cm,球目前在E点位置,AE=35cm,如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.