题目内容
 如图,平行四边形ABCD中,对角线AC、BD交于O,E是AO中点,BE的延长线与BD的平行线AF交于点F.
如图,平行四边形ABCD中,对角线AC、BD交于O,E是AO中点,BE的延长线与BD的平行线AF交于点F.(1)求证:AF=BO.
(2)当平行四边形ABCD满足条件
(3)在上一步的条件下,证明四边形AODF是矩形.
考点:矩形的判定,平行四边形的性质
专题:
分析:(1)证得△FAE和△BOE全等后即可证得AF=BO;
(2)得到四边形AODF是平行四边形后添加一个条件使得平行四边形成为矩形即可;
(3)利用有一个角是直角的平行四边形是矩形判定矩形即可.
(2)得到四边形AODF是平行四边形后添加一个条件使得平行四边形成为矩形即可;
(3)利用有一个角是直角的平行四边形是矩形判定矩形即可.
解答:(1)证明:∵AF∥BD,
∴∠AFB=∠OBF,
∵E是AO中点,
∴AE=OE,
在△FAE和△BOE中,
,
∴△FAE≌△BOE(ASA),
∴AF=BO;
(2)解:添加条件AC⊥BD即可使得四边形AODF是矩形;
(3)证明:∵AF=BO,BO=DO,
∴AF=DO,
∵AF∥BD,
∴四边形AODF为平行四边形,
∵AC⊥BD,
∴四边形AODF为矩形.
∴∠AFB=∠OBF,
∵E是AO中点,
∴AE=OE,
在△FAE和△BOE中,
|
∴△FAE≌△BOE(ASA),
∴AF=BO;
(2)解:添加条件AC⊥BD即可使得四边形AODF是矩形;
(3)证明:∵AF=BO,BO=DO,
∴AF=DO,
∵AF∥BD,
∴四边形AODF为平行四边形,
∵AC⊥BD,
∴四边形AODF为矩形.
点评:本题考查了矩形的判定、全等三角形的判定及性质等知识,解题的关键是证得第1问,这是下一步解题的基础,难度不大.

练习册系列答案
相关题目
 如图,P为∠AOB内一定点,M、N分别是射线OA、OB上一点,当△PMN周长最小时,∠OPM=50°,则∠AOB=( )
如图,P为∠AOB内一定点,M、N分别是射线OA、OB上一点,当△PMN周长最小时,∠OPM=50°,则∠AOB=( )| A、40° | B、45° |
| C、50° | D、55° |
 如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC,点P是直线AO上任意一点,求证:AO⊥BC,PB=PC.
如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC,点P是直线AO上任意一点,求证:AO⊥BC,PB=PC.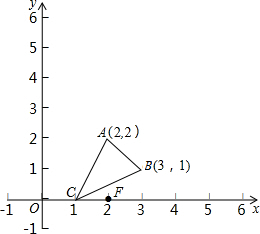 如图,△ABC的三个顶点坐标分别为A(2,2),B(3,1),C(1,0),试将△ABC放大,使放大后的△DEF与△ABC对应边之比为2:1,并指出其对应边AB与DE有何位置关系?并说明理由.
如图,△ABC的三个顶点坐标分别为A(2,2),B(3,1),C(1,0),试将△ABC放大,使放大后的△DEF与△ABC对应边之比为2:1,并指出其对应边AB与DE有何位置关系?并说明理由. 如图,在等腰三角形ABC中,请根据图中所给数据求出tanB.
如图,在等腰三角形ABC中,请根据图中所给数据求出tanB.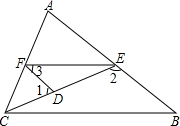 如图,已知∠1+∠2=180°,∠3=∠B,且∠AFE=50°,求∠ACB的度数.
如图,已知∠1+∠2=180°,∠3=∠B,且∠AFE=50°,求∠ACB的度数. 如图,数轴上的点A和B所表示的数分别是a、b,且|a|>|b|,如果a、b异号,在图中标出表示数0的点O的大致位置.
如图,数轴上的点A和B所表示的数分别是a、b,且|a|>|b|,如果a、b异号,在图中标出表示数0的点O的大致位置.