题目内容
 如图,矩形ABCD为台球桌面,AD=280cm,AB=140cm,球目前在E点位置,AE=35cm,如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
如图,矩形ABCD为台球桌面,AD=280cm,AB=140cm,球目前在E点位置,AE=35cm,如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.(1)求证:△BEF∽△CDF;
(2)求CF的长.
考点:相似三角形的应用
专题:
分析:(1)根据题意得出∠EFB=∠DFC,进而利用相似三角形的判定方法求出即可;
(2)利用相似三角形的性质得出FC的长即可.
(2)利用相似三角形的性质得出FC的长即可.
解答:(1)证明:∵∠EFG=∠DFG,
∴∠EFB=∠DFC,
又∵∠B=∠C,
∴△BEF∽△CDF;
(2)解:∵△BEF∽△CDF,
∴
=
,
设FC=xcm,则
=
,
解得:x=160,
答:CF的长为160cm.
∴∠EFB=∠DFC,
又∵∠B=∠C,
∴△BEF∽△CDF;
(2)解:∵△BEF∽△CDF,
∴
| BE |
| DC |
| FB |
| FC |
设FC=xcm,则
| 105 |
| 140 |
| 280-x |
| x |
解得:x=160,
答:CF的长为160cm.
点评:此题主要考查了相似三角形的判定与性质,得出△BEF∽△CDF是解题关键.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,点A、B的坐标分别为(-3,0)、(0,4),以点A为圆心,以AB长为半径画弧交x轴上点C,则点C的坐标为( )
如图,在平面直角坐标系中,点A、B的坐标分别为(-3,0)、(0,4),以点A为圆心,以AB长为半径画弧交x轴上点C,则点C的坐标为( )| A、(5,0) |
| B、(2,0) |
| C、(-8,0) |
| D、(2,0)或(-8,0) |
绝对值等于5的数是( )
| A、-5 | ||
| B、-5或5 | ||
| C、5 | ||
D、
|
如果不等式组
的解集是x>2,则m的取值范围是 ( )
|
| A、m≥2 | B、m≤2 |
| C、m=2 | D、m<2 |
下列各数中无理数有( )
3.141,-
,
,π,0,4.2
,0.1010010001.
3.141,-
| 22 |
| 7 |
| 3 | -27 |
| •• |
| 17 |
| A、1个 | B、2个 | C、3个 | D、4个 |
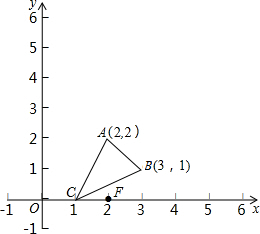 如图,△ABC的三个顶点坐标分别为A(2,2),B(3,1),C(1,0),试将△ABC放大,使放大后的△DEF与△ABC对应边之比为2:1,并指出其对应边AB与DE有何位置关系?并说明理由.
如图,△ABC的三个顶点坐标分别为A(2,2),B(3,1),C(1,0),试将△ABC放大,使放大后的△DEF与△ABC对应边之比为2:1,并指出其对应边AB与DE有何位置关系?并说明理由. 如图,数轴上的点A和B所表示的数分别是a、b,且|a|>|b|,如果a、b异号,在图中标出表示数0的点O的大致位置.
如图,数轴上的点A和B所表示的数分别是a、b,且|a|>|b|,如果a、b异号,在图中标出表示数0的点O的大致位置.