题目内容
18.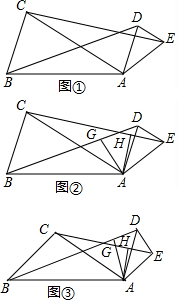 如图①,在△ABC和△ADE中,AD=$\frac{1}{2}$AB,AE=$\frac{1}{2}$AC,∠BAC=∠DAE,连接BD、CE.
如图①,在△ABC和△ADE中,AD=$\frac{1}{2}$AB,AE=$\frac{1}{2}$AC,∠BAC=∠DAE,连接BD、CE.(1)若AB=AC,
①求证:BD=CE;
②在BD、CE上截取DG=$\frac{1}{4}$BD,EH=$\frac{1}{4}$CE,连接AG、AH得到图②,猜想AG与AH的数量关系、∠GAH与∠BAC的数量关系,并证明你的猜想;
(2)如图③若AB=$\frac{3}{2}$AC,其它条件不变,猜想AG与AH的数量关系、∠GAH与∠BAC的数量关系,直接写出你的猜想,不必证明.
分析 (1)①根据SAS判定△BAD≌△CAE,再根据全等三角形的对应边相等,得出结论即可;②根据全等三角形的性质,得出∠ABG=∠ACH,BG=CH,进而判定△BAG≌△CAH,即可得出结论:AG与AH的数量关系为AG=AH;∠GAH与∠BAC的数量关系为∠GAH=∠BAC.
(2)先判定△BAD∽△CAE,再根据相似三角形的性质,得出$\frac{AB}{AC}$=$\frac{BG}{CH}$=$\frac{3}{2}$,∠ABG=∠ACH,最后判定△BAG∽△CAH,即可得出结论:AG与AH的数量关系为AG=$\frac{3}{2}$AH;∠GAH与∠BAC的数量关系为∠GAH=∠BAC.
解答  解:(1)如图①∵AD=$\frac{1}{2}$AB,AE=$\frac{1}{2}$AC,AB=AC,
解:(1)如图①∵AD=$\frac{1}{2}$AB,AE=$\frac{1}{2}$AC,AB=AC,
∴AD=AE,
∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△BAD≌△CAE(SAS),
∴BD=CE;
②AG与AH的数量关系为AG=AH;∠GAH与∠BAC的数量关系为∠GAH=∠BAC.
证明:如图②∵△BAD≌△CAE,
∴∠ABG=∠ACH,
∵DG=$\frac{1}{4}$BD,EH=$\frac{1}{4}$CE,BD=CE,
∴BG=CH,
在△BAG和△CAH中,
$\left\{\begin{array}{l}{AB=AC}\\{∠ABG=∠ACH}\\{BG=CH}\end{array}\right.$,
∴△BAG≌△CAH(SAS),
∴AG=AH,∠BAG=∠CAH,
∴∠GAH=∠BAC;
(2)AG与AH的数量关系为AG=$\frac{3}{2}$AH;∠GAH与∠BAC的数量关系为∠GAH=∠BAC.
理由:如图③,根据AD=$\frac{1}{2}$AB,AE=$\frac{1}{2}$AC,AB=$\frac{3}{2}$AC,∠BAC=∠DAE,
可得$\frac{AB}{AC}$=$\frac{AD}{AE}$=$\frac{3}{2}$,∠BAD=∠CAE,
∴△BAD∽△CAE,
∴∠ABG=∠ACH,BD=$\frac{3}{2}$CE,
∵DG=$\frac{1}{4}$BD,EH=$\frac{1}{4}$CE,
∴BG=$\frac{3}{2}$CH,
在△BAG和△CAH中,
$\frac{AB}{AC}$=$\frac{BG}{CH}$=$\frac{3}{2}$,∠ABG=∠ACH,
∴△BAG∽△CAH,
∴$\frac{AG}{AH}$=$\frac{AB}{AC}$=$\frac{3}{2}$,∠BAG=∠CAH,
∴AG=$\frac{3}{2}$AH,∠GAH=∠BAC.
点评 本题主要考查了三角形的综合应用,解决问题的关键是掌握全等三角形的判定与性质以及相似三角形的判定与性质,解题时注意:两边及其夹角分别对应相等的两个三角形全等;两组对应边的比相等且夹角对应相等的两个三角形相似.

 名校课堂系列答案
名校课堂系列答案①两个有理数相加,和一定大于每一个加数
②一个正数与一个负数相加得正数
③两个负数和的绝对值一定等于它们绝对值的和
④两个正数相加,和为正数
⑤正数加负数,其和一定等于0.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
 有理数a,b,c在数轴上的位置如图所示,下面结论正确的是( )
有理数a,b,c在数轴上的位置如图所示,下面结论正确的是( )| A. | c>a | B. | c>0 | C. | |a|<|b| | D. | a-c<0 |
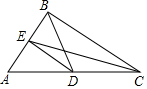 如图,在△ABC中,∠ABC=100°,∠ACB=20°,CE是∠ACB的平分线,D是AC上的一点且BD=ED,若∠CBD=20°,则∠CED的度数为10°.
如图,在△ABC中,∠ABC=100°,∠ACB=20°,CE是∠ACB的平分线,D是AC上的一点且BD=ED,若∠CBD=20°,则∠CED的度数为10°.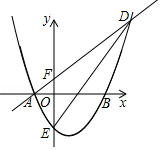 如图,抛物线y=ax2+bx+c与x轴交于A(-1,0)和B(3,0)两点,交y轴于点E(0,-3).
如图,抛物线y=ax2+bx+c与x轴交于A(-1,0)和B(3,0)两点,交y轴于点E(0,-3).
 某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计表,根据统计图提供的信息解决下列问题:
某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计表,根据统计图提供的信息解决下列问题: