��Ŀ����
7����ͼ��?ABCD��ƽ��ֱ������ϵ�У�AD=6����OA��OB�ij��ǹ���x��һԪ���η���x2-7x+12=0������������OA��OB����1����AB�ij���
��2��������P�ӵ�B��������ÿ��1����λ���ȵ��ٶ���B��A�����˶�����P��x��Ĵ��߽�x���ڵ�E����S��PBE=$\frac{1}{9}$S��ABO�����ʱ��P�����ꣻ
��3���ڣ�2���У�������P�����A����AD������ԭ�ٶȼ������D�˶���PE��DC�߽��ڵ�F����ͼ2���Ƿ����������tֵ��ʹ��S��PBE=$\frac{1}{9}$S��ABO�������ڣ����tֵ���������ڣ���˵�����ɣ�
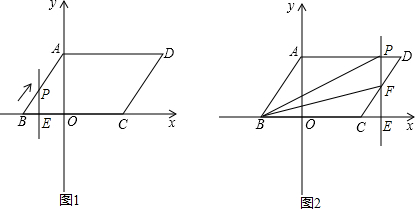
���� ��1���Ƚ�һԪ���η���x2-7x+12=0���OA��OB�ij��������ù��ɶ����������AB�ij���
��2�����ɣ�1����OA��OB�ij��ó�A��B��������꣬�ٸ���ƽ���ı��ε����ʵõ�C��D��������꣬Ȼ�����ô���ϵ�����������CD������ֱ�ߵĺ�����ϵʽ��
��3������PE��OA���ó���PBE�ס�ABO���г�����ʽ���õ�BE��PE�ij����ٸ���S��PBE=$\frac{1}{9}$S��ABO���г�����t�ķ��̣��ⷽ�̼��ɣ�
��4������AP=t-5���ó�BE=t-2��CE=t-8��PD=11-t���ٸ��ݡ�PDF�ס�ECF���ó�PF=$\frac{44-4t}{3}$��Ȼ����S��PBF=$\frac{1}{9}$S��ABO�г�����t�ķ��̣��ⷽ�̼���
��� �⣺��1����OA��OB�ij��ǹ���x��һԪ���η���x2-7x+12=0����������
�ࣨx-3����x-4��=0����OA��OB��
��OA=4��OB=3��
�ɹ��ɶ�������AB=5��
��2����OA=4��OB=3��
��A��������0��4����B���������-3��0����
��?ABCD��ƽ��ֱ������ϵ�У�AD=6��
��D��������6��4����BC=AD=6��
��OC=BC-OB=3��
��C��������3��0����
��ֱ��CD�Ľ���ʽΪy=kx+b����
6k+b=4��3k+b=0��
k=$\frac{4}{3}$��b=-4��
��ֱ��CD�Ľ���ʽΪy=$\frac{4}{3}$x-4��
��3����PE��OA��
���PBE�ס�ABO��
��BE��BO=PE��AO=BP��BA����BE��3=PE��4=t��5��
��BE=$\frac{3}{5}$t��PE=$\frac{4}{5}$t��
��S��PBE=$\frac{1}{9}$S��ABO��
��$\frac{1}{2}$��$\frac{3}{5}$t��$\frac{4}{5}$t=$\frac{1}{9}$��$\frac{1}{2}$��3��4��
���t=��$\frac{5}{3}$����ֵ��ȥ����
��t=$\frac{5}{3}$��
��BE=1��PE=$\frac{4}{3}$
��OE=OB-BE=3-1=2��
���ʱ��P������Ϊ��-2��$\frac{4}{3}$����
��4������������tֵ���ܹ�ʹ��S��PBF=$\frac{1}{9}$S��ABO���������£�
��ͼ2����BA+AP=t��
��AP=t-5��
��BE=BO+OE=3+t-5=t-2��CE=OE-OC=t-5-3=t-8��PD=AD-AP=6-t+5=11-t��
��PD��CE��
���PDF�ס�ECF��
��PD��EC=PF��EF��
��PD����PD+EC��=PF����PF+EF����
��11-t������11-t+t-8��=PF��4��
��PF=$\frac{44-4t}{3}$��
��S��PBF=$\frac{1}{9}$S��ABO��
��$\frac{1}{2}$PF��BE=$\frac{1}{9}$��$\frac{1}{2}$��3��4��
��$\frac{1}{2}$��$\frac{44-4t}{3}$����t-2��=$\frac{2}{3}$��
��������t2-13t+23=0��
���t=$\frac{13+\sqrt{77}}{2}$��t=$\frac{13-\sqrt{77}}{2}$���ᣩ
����t=$\frac{13+\sqrt{77}}{2}$��
���� �������ı����ۺ��⣬�漰��ƽ���ı��ε����ʣ���һԪ���η��̣����ɶ���������ϵ������ֱ�ߵĽ���ʽ�������ε���������������ε��������ж����������⡢�����������֪ʶ���������ú�t�Ĵ���ʽ��ȷ��ʾ�������εĵ�����ǽ���Ĺؼ���

 ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�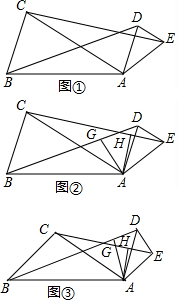 ��ͼ�٣��ڡ�ABC�͡�ADE�У�AD=$\frac{1}{2}$AB��AE=$\frac{1}{2}$AC����BAC=��DAE������BD��CE��
��ͼ�٣��ڡ�ABC�͡�ADE�У�AD=$\frac{1}{2}$AB��AE=$\frac{1}{2}$AC����BAC=��DAE������BD��CE�� һ��أ���C���߶�AB�ֳ������߶�AC��BC�����$\frac{AC}{AB}$=$\frac{BC}{AC}$����ô���߶�AB����C�ƽ�ָ��C�����߶�AB�Ļƽ�ָ�㣬AC��AB�ıȽ����ƽ�ȣ������ƽ�ȣ�
һ��أ���C���߶�AB�ֳ������߶�AC��BC�����$\frac{AC}{AB}$=$\frac{BC}{AC}$����ô���߶�AB����C�ƽ�ָ��C�����߶�AB�Ļƽ�ָ�㣬AC��AB�ıȽ����ƽ�ȣ������ƽ�ȣ�