题目内容
6．画出数轴，在数轴上表示下列各数，并用“＜”连接．3.5，-$\frac{3}{4}$，-1$\frac{1}{3}$，4，0，-2.5．
分析 在数轴上表示出各数，从左到右用“＜”连接起来即可．
解答 解：如图所示，
-2.5$＜-1\frac{1}{3}$＜-$\frac{3}{4}$＜0＜3.5＜4．
点评 本题考查的是有理数的大小比较，熟知数轴上右边的数总比左边的大是解答此题的关键．
练习册系列答案
相关题目
16．一元二次方程x2-2x-3=0 的两根分别是x1、x2，则x1+x2的值是（ ）
| A． | 3 | B． | 2 | C． | -3 | D． | -2 |
14．观察下列等式：31=3，32=9，33=27，34=81，35=243，36=729，37=2187…解答下列问题：3+32+33+34+…+32014的末位数字是（ ）
| A． | 2 | B． | 3 | C． | 7 | D． | 9 |
1．在创建全国文明城市活动中，衢州市园林部分为了扩大市区的绿化面积，进行了大量的树木移栽，如表记录的是在相同条件下移栽某种幼树的棵树和成活棵树：
请根据表中数据估计，现园林部门移栽5000棵这种幼树，大约能成活4500棵．
| 移栽棵树 | 100 | 500 | 1000 | 5000 | 10000 |
| 成活棵树 | 89 | 458 | 910 | 4498 | 9000 |
11．已知二次函数y=ax2+bx+c中，其函数y与自变量x之间的部分对应值如表所示：
（1）顶点坐标为（2，0）；
（2）若将此图象沿x轴向右平移3个单位，请写出平移后图象所对应的函数关系式：y=（x-5）2；
（3）设点P1（m，y1）、P2（m+1，y2）、P3（m+2，y3）都在二次函数y=ax2+bx+c的图象上，问：当m＜-3时，y1、y2、y3的值一定能作为同一个三角形三边的长吗？为什么？
| x | … | 0 | 1 | 2 | 3 | 4 | 5 | … |
| y | … | 4 | 1 | 0 | 1 | 4 | 9 | … |
（2）若将此图象沿x轴向右平移3个单位，请写出平移后图象所对应的函数关系式：y=（x-5）2；
（3）设点P1（m，y1）、P2（m+1，y2）、P3（m+2，y3）都在二次函数y=ax2+bx+c的图象上，问：当m＜-3时，y1、y2、y3的值一定能作为同一个三角形三边的长吗？为什么？
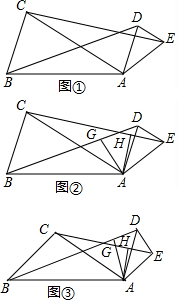如图①，在△ABC和△ADE中，AD=$\frac{1}{2}$AB，AE=$\frac{1}{2}$AC，∠BAC=∠DAE，连接BD、CE．
一般地，点C把线段AB分成两条线段AC和BC，如果$\frac{AC}{AB}$=$\frac{BC}{AC}$，那么称线段AB被点C黄金分割，点C叫做线段AB的黄金分割点，AC与AB的比叫做黄金比．请计算黄金比．