Question

2．已知二次函数y=2x²+4x-6．
（1）将其化成y=a（x-h）²+k的形式；
（2）写出图象的开口方向、对称轴、顶点坐标；
（3）求图象与两坐标轴的交点坐标；
（4）画出函数图象；
（5）说明其图象与抛物线y=2x²的关系；
（6）当x取何值时，函数y由最值？其最值是多少？
（7）求函数图象与两坐标轴的交点所组成的三角形的面积．

Answer 1

分析 （1）利用配方法先提出二次项系数，再加上一次项系数的一半的平方来凑完全平方式，把一般式转化为顶点式．
（2）根据a的符号判断抛物线的开口方向；根据顶点式可求顶点坐标及对称轴．
（3）分别把x=0和y=0代入函数的解析式中即可求解；
（4）根据顶点坐标和交点坐标画出函数图象；
（5）根据二次函数的a的值即可得到图象与抛物线y=2x²的关系；
（6）根据二次函数的性质和顶点坐标求得；
（7）根据交点坐标得出三角形底边和高，根据三角形面积求得．

解答 解：（1）y=2x²+4x-6，
y=2（x²+2x）-6，
y=2（x²+2x+1-1）-6，
y=2（x+1）²-8．
（2）∵a=2＞0，图象开口向上；
∵y=2（x+1）²-8．
∵对称轴是x=-1，顶点坐标是（-1，-8）．
（3）当x=0时，y=-6，
当y=0时，2x²+4x-6=0，
则x=-3或x=1，
则与坐标轴交于点（1、0），（-3、0），（0，6）；
（4）画出函数图象如图：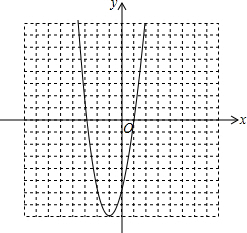

（5）∵二次项系数相同，
∴图象与抛物线y=2x²的图象开口大小相同，方向相同；
（6）当x=-1时，有最小值y=-8；
（7）∵与坐标轴交于点（1、0），（-3、0），（0，6），
∴函数图象与两坐标轴的交点所组成的三角形的面积：$\frac{1}{2}$×（1+3）×6=12．

点评 本题考查了二次函数的性质：二次函数y=ax²+bx+c（a≠0）的图象为抛物线；对称轴为直线x=-$\frac{b}{2a}$；抛物线与y轴的交点坐标为（0，c）；当a＞0时，抛物线开口向上，当x＜-$\frac{b}{2a}$时，y随x的增大而减小；x＞-$\frac{b}{2a}$时，y随x的增大而增大；x=-$\frac{b}{2a}$时，y取得最小值$\frac{4ac-{b}^{2}}{4a}$，即顶点是抛物线的最低点；当a＜0时，抛物线开口向下，x＜=-$\frac{b}{2a}$时，y随x的增大而增大；x＞-$\frac{b}{2a}$时，y随x的增大而减小；x=-$\frac{b}{2a}$时，y取得最大值$\frac{4ac-{b}^{2}}{4a}$，即顶点是抛物线的最高点．