Question

13．已知，如图，AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交于点P，∠COB=2∠PCB，AC=PC．
（1）求证：OC⊥CP；
（2）求cos∠PAC的值；
（3）点M是弧AB的中点，CM交AB于点N，若AB=6，求MN•MC的值．

Answer 1

分析 （1）已知C在圆上，故只需证明OC与PC垂直即可；根据圆周角定理，易得∠PCB+∠OCB=90°，即OC⊥CP；
（2）AB是直径；故只需证明BC与半径相等即可；继而求得cos∠PAC的值；
（3）连接MA，MB，由圆周角定理可得∠ACM=∠BCM，进而可得△MBN∽△MCB，故BM²=MN•MC；又由△ABM是等腰直角三角形，即可求得BM的值，继而求得答案．

解答 （1）证明：∵OA=OC，
∴∠A=∠ACO．
又∵∠COB=2∠A，∠COB=2∠PCB，
∴∠A=∠ACO=∠PCB．
又∵AB是⊙O的直径，
∴∠ACO+∠OCB=90°．
∴∠PCB+∠OCB=90°．
即OC⊥CP；

（2）证明：∵AC=PC，
∴∠A=∠P，
∴∠A=∠ACO=∠PCB=∠P．
又∵∠COB=∠A+∠ACO，∠CBO=∠P+∠PCB，
∴∠COB=∠CBO，
∴BC=OC，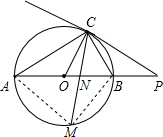
∴BC=$\frac{1}{2}$AB，
∴∠A=30°，
∴cos∠PAC=$\frac{\sqrt{3}}{2}$；

（3）解：连接MA，MB，
∵点M是$\widehat{AB}$的中点，
∴$\widehat{AM}$=$\widehat{BM}$，
∴∠ACM=∠BCM．
∵∠ACM=∠ABM，
∴∠BCM=∠ABM．
∵∠BMN=∠BMC，
∴△MBN∽△MCB．
∴$\frac{BM}{MC}=\frac{MN}{BM}$．
∴BM²=MN•MC．
又∵AB是⊙O的直径，$\widehat{AM}$=$\widehat{BM}$，
∴∠AMB=90°，AM=BM．
∵AB=6，
∴BM=3$\sqrt{2}$．
∴MN•MC=BM²=18．

点评 此题考查了相似三角形的判定与性质、圆周角定理、垂径定理以及三角函数等知识．注意准确作出辅助线是解此题的关键．