题目内容
4. 如图,在△AOC和△BOC中,若∠AOC=∠BOC,添加一个条件AO=BO,使得△AOC≌△BOC.
如图,在△AOC和△BOC中,若∠AOC=∠BOC,添加一个条件AO=BO,使得△AOC≌△BOC.
分析 添加AO=BO,再加上条件∠AOC=∠BOC,公共边CO=CO可利用SAS定理判定△AOC≌△BOC.
解答 解:添加AO=BO,
∵在△AOC和△BOC中$\left\{\begin{array}{l}{AO=BO}\\{∠AOC=∠BOC}\\{CO=CO}\end{array}\right.$,
∴△AOC≌△BOC(SAS),
故答案为:AO=BO.
点评 此题主要考查了全等三角形的判定,关键是掌握判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
15.一个三角形的两边长为4和6,第三边的边长是方程(x-2)(x-7)=0的两根,则这个三角形的周长是( )
| A. | 12 | B. | 12或17 | C. | 17 | D. | 19 |
12.a为有理数,下列说法中正确的是( )
| A. | -a一定是负数 | B. | -a2一定是负数 | C. | (-a)3一定是负数 | D. | |a|一定不是负数 |
9.若a与2014的互为倒数,则a的值是( )
| A. | -2014 | B. | 2014 | C. | -$\frac{1}{2014}$ | D. | $\frac{1}{2014}$ |
16. 如图,一圆弧形钢梁的拱高CD为8m,跨径AB为40m,则这钢梁圆弧的半径是( )
如图,一圆弧形钢梁的拱高CD为8m,跨径AB为40m,则这钢梁圆弧的半径是( )
 如图,一圆弧形钢梁的拱高CD为8m,跨径AB为40m,则这钢梁圆弧的半径是( )
如图,一圆弧形钢梁的拱高CD为8m,跨径AB为40m,则这钢梁圆弧的半径是( )| A. | 28m | B. | 29m | C. | 30m | D. | 31m |
13.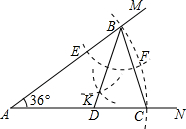 如图,小明作图如下:
如图,小明作图如下:
(1)用量角器作∠MAN=36°;
(2)以A为圆心适当长为半径作圆弧,分别交AM,AN于B,C两点,连结BC;
(3)以B为圆心适当长为半径作圆弧,分别交AB,BC于E,F两点,再分别以E,F为圆心大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点K,连结BK并延长交AC于点D.
若AD=a,则由以上作图可得AB为( )
 如图,小明作图如下:
如图,小明作图如下:(1)用量角器作∠MAN=36°;
(2)以A为圆心适当长为半径作圆弧,分别交AM,AN于B,C两点,连结BC;
(3)以B为圆心适当长为半径作圆弧,分别交AB,BC于E,F两点,再分别以E,F为圆心大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点K,连结BK并延长交AC于点D.
若AD=a,则由以上作图可得AB为( )
| A. | $\frac{\sqrt{5}-1}{2}$a | B. | $\frac{3-\sqrt{5}}{2}$a | C. | $\frac{\sqrt{5}+1}{2}a$ | D. | $\frac{3+\sqrt{5}}{2}$a |
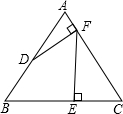 如图,已知:等边三角形ABC,点D是AB的中点,过点D作DF⊥AC,垂足为F,过点F作FE⊥BC,垂足为E,若三角形ABC的边长为4.则线段BE的长为$\frac{5}{2}$.
如图,已知:等边三角形ABC,点D是AB的中点,过点D作DF⊥AC,垂足为F,过点F作FE⊥BC,垂足为E,若三角形ABC的边长为4.则线段BE的长为$\frac{5}{2}$.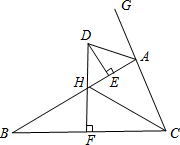 如图,△ABC中,AB>AC,延长CA至点G,边BC的垂直平分线DF与∠BAG的角平分线交于点D,与AB交于点H,F为垂足,DE⊥AB于E.下列说法正确的是③.(填序号)
如图,△ABC中,AB>AC,延长CA至点G,边BC的垂直平分线DF与∠BAG的角平分线交于点D,与AB交于点H,F为垂足,DE⊥AB于E.下列说法正确的是③.(填序号)