题目内容
9.在数列$\frac{1}{2011}$,$\frac{2}{2010}$,$\frac{3}{2009}$,…,$\frac{2010}{2}$,$\frac{2011}{1}$中共有6个整数.分析 通过观察可发现将这组数列首尾交换重新排列为:$\frac{2011}{1}$,$\frac{2010}{2}$,…,$\frac{3}{2009}$,$\frac{2}{2010}$,$\frac{1}{2011}$,观察这组数据得到通项公式为:$\frac{2012-n}{n}$,再计算即可得出答案.
解答 解:将这组数列首尾交换重新排列为:$\frac{2011}{1}$,$\frac{2010}{2}$,…,$\frac{3}{2009}$,$\frac{2}{2010}$,$\frac{1}{2011}$,观察这组数据得到通项公式为:$\frac{2012-n}{n}$,
∴当$\frac{2012-n}{n}$为整数时,即$\frac{2012}{n}$为整数,
∴n=1,2,4,503,1006,2012,
∴在数列$\frac{1}{2011}$,$\frac{2}{2010}$,$\frac{3}{2009}$,…,$\frac{2010}{2}$,$\frac{2011}{1}$中共有6个整数,
故答案为:6.
点评 本题主要考查学生的观察能力以及对规律的认识和总结,并能灵活运用.

练习册系列答案
相关题目
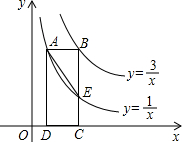 如图,矩形ABCD的一边CD在x轴上,顶点A、B分别落在双曲线y=$\frac{1}{x}$(x>0)、y=$\frac{3}{x}$(x>0)上,边BC交双曲线y=$\frac{1}{x}$(x>0)于点E,连接AE,则△ABE的面积为$\frac{2}{3}$.
如图,矩形ABCD的一边CD在x轴上,顶点A、B分别落在双曲线y=$\frac{1}{x}$(x>0)、y=$\frac{3}{x}$(x>0)上,边BC交双曲线y=$\frac{1}{x}$(x>0)于点E,连接AE,则△ABE的面积为$\frac{2}{3}$.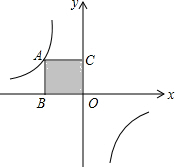 如图,点A是反比例函数y=$\frac{k}{x}$图象上的一个动点,过点A作AB⊥x轴,AC⊥y轴,垂足点分别为B、C,矩形ABOC的面积为4,则k=-4.
如图,点A是反比例函数y=$\frac{k}{x}$图象上的一个动点,过点A作AB⊥x轴,AC⊥y轴,垂足点分别为B、C,矩形ABOC的面积为4,则k=-4.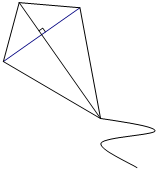 如图,小明将一根长为1.4米的竹条截为两段,并互相垂直固定,作为风筝的龙骨,制作成了一个面积为0.24米2的风筝.请你计算一下将竹条截成长度分别为多少的两段?
如图,小明将一根长为1.4米的竹条截为两段,并互相垂直固定,作为风筝的龙骨,制作成了一个面积为0.24米2的风筝.请你计算一下将竹条截成长度分别为多少的两段?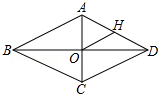 如图,菱形ABCD中,对角线AC、BC相交于点O,H为AD边中点,菱形ABCD的周长为28,求OH的长?
如图,菱形ABCD中,对角线AC、BC相交于点O,H为AD边中点,菱形ABCD的周长为28,求OH的长?