��Ŀ����
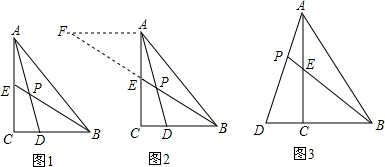
17���Ķ�������ϣ�С���������һ�����⣺��ͼ1���ڡ�ABC�У���ACB=90�㣬BE��AC���ϵ����ߣ���D��BC���ϣ�CD��BD=1��2��AD��BE�ཻ�ڵ�P����$\frac{AP}{PD}$��ֵ��
С껷��֣�����A��AF��BC����BE���ӳ����ڵ�F��ͨ�������AEF�����������ͼ����ܹ�ʹ����õ��������ͼ2����
��ش�$\frac{AP}{PD}$��ֵΪ$\frac{3}{2}$��
�ο�С�˼������ķ�����������⣺
��ͼ 3���ڡ�ABC�У���ACB=90�㣬��D��BC���ӳ����ϣ�AD��AC���ϵ�����BE���ӳ��߽��ڵ�P��DC��BC��AC=1��2��3��
��1����$\frac{AP}{PD}$��ֵ��
��2����CD=2����BP=6��
���� ��֤��AEF�ա�CEB������AF=BC����CD=k����DB=2k��AF=BC=3k����AF��BC�ɵá�APF�ס�DPB��Ȼ��������������ε����ʾͿ����$\frac{AP}{PD}$��ֵ��
������⣺��1������A��AF��DB����BE���ӳ����ڵ�F����DC=k����DC��BC=1��2��BC=2k��DB=DC+BC=3k����֤��AEF�ա�CEB������EF=BE��AF=BC=2k����֤��AFP�ס�DBP��Ȼ��������������ε����ʾͿ����$\frac{AP}{PD}$��ֵ��
��2����CD=2ʱ�����������BC��AC��EC��EB��EF��BF��ֵ��Ȼ�����$\frac{FP}{BP}$��ֵ���$\frac{BF}{BP}$���Ϳ����BP��ֵ��
��� �⣺$\frac{AP}{PD}$��ֵΪ$\frac{3}{2}$��
��ʾ����֤��AEF�ա�CEB������AF=BC��
��CD=k����DB=2k��AF=BC=3k��
��AF��BC�ɵá�APF�ס�DPB��
���ɵõ�$\frac{AP}{PD}$=$\frac{AF}{BD}$=$\frac{3}{2}$��
�ʴ�Ϊ��$\frac{3}{2}$��
������⣺
��1������A��AF��DB����BE���ӳ����ڵ�F����ͼ��
��DC=k��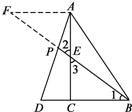 ��DC��BC=1��2��BC=2k��DB=DC+BC=3k��
��DC��BC=1��2��BC=2k��DB=DC+BC=3k��
��E��AC�е㣬
��AE=CE��
��AF��DB��
���F=��1��
�ڡ�AEF�͡�CEB�У�
$\left\{\begin{array}{l}{��F=��1}\\{��2=��3}\\{AE=CE}\end{array}\right.$��
���AEF�ա�CEB��
��EF=BE��AF=BC=2k��
��AF��DB��
���AFP�ס�DBP��
��$\frac{AP}{DP}$=$\frac{FP}{BP}$=$\frac{AF}{DB}$=$\frac{2k}{3k}$=$\frac{2}{3}$��
��$\frac{AP}{PD}$��ֵΪ$\frac{2}{3}$��
��2����CD=2ʱ��BC=4��AC=6��
��EC=$\frac{1}{2}$AC=3��EB=$\sqrt{E{C}^{2}+B{C}^{2}}$=5��
��EF=BE=5��BF=10��
��$\frac{FP}{BP}$=$\frac{2}{3}$����֤����
��$\frac{BF}{BP}$=$\frac{5}{3}$��
��BP=$\frac{3}{5}$BF=$\frac{3}{5}$��10=6��
�ʴ�Ϊ6��
���� ������Ҫ���������������ε��ж������ʡ�ȫ�������ε��ж������ʡ����ɶ�����֪ʶ������е㣬��ƽ���߹���ȫ���������ǽ������Ĺؼ���

 ��У����ϵ�д�
��У����ϵ�д�| A�� | x��2 | B�� | x��2 | C�� | x��2 | D�� | x��2 |
 ��ͼ����������ABC����DE�۵���ʹ��A����BC�ϵĵ�F������DE��BC������B=65�㣬���BDF=50�㣮
��ͼ����������ABC����DE�۵���ʹ��A����BC�ϵĵ�F������DE��BC������B=65�㣬���BDF=50�㣮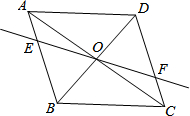 ��ͼ����?ABCD�У��Խ���AC��BD���ڵ�O��������O��ֱ�߽�AB��E����CD��F��
��ͼ����?ABCD�У��Խ���AC��BD���ڵ�O��������O��ֱ�߽�AB��E����CD��F�� ��ͼ����ABC��A��ʱ����תʹ��C������BC ���ϵ�F ��������ڽ��ۢ�AC=AF���ڡ�FAB=��EAB�� ��EF=BC���ܡ�EAB=��FAC��������ȷ���۵ĸ����ǣ�������
��ͼ����ABC��A��ʱ����תʹ��C������BC ���ϵ�F ��������ڽ��ۢ�AC=AF���ڡ�FAB=��EAB�� ��EF=BC���ܡ�EAB=��FAC��������ȷ���۵ĸ����ǣ�������