题目内容
14.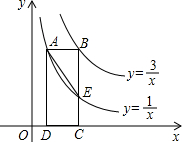 如图,矩形ABCD的一边CD在x轴上,顶点A、B分别落在双曲线y=$\frac{1}{x}$(x>0)、y=$\frac{3}{x}$(x>0)上,边BC交双曲线y=$\frac{1}{x}$(x>0)于点E,连接AE,则△ABE的面积为$\frac{2}{3}$.
如图,矩形ABCD的一边CD在x轴上,顶点A、B分别落在双曲线y=$\frac{1}{x}$(x>0)、y=$\frac{3}{x}$(x>0)上,边BC交双曲线y=$\frac{1}{x}$(x>0)于点E,连接AE,则△ABE的面积为$\frac{2}{3}$.
分析 首先根据双曲线的解析式设出点B的坐标,然后表示出点A和点E的坐标,用矩形ABCD的面积减去梯形ADCE的面积即可得到答案.
解答 解:∵点B在y=$\frac{3}{x}$上,
∴设点B的坐标为(a,$\frac{3}{a}$),
∴点A的纵坐标为$\frac{3}{a}$,点E的横坐标为a,
∵点A在y=$\frac{1}{x}$上,
∴点A的横坐标为$\frac{a}{3}$,
∵A,B分别落在双曲线y=$\frac{1}{x}$、y=$\frac{3}{x}$上,
∴矩形AFOD的面积为1,矩形BFDC的面积为3,
∴矩形BADC的面积为2,
∴S△ABE=S矩形BADC-S梯形AECD=2-$\frac{1}{2}$(a-$\frac{a}{3}$)×($\frac{3}{a}$+$\frac{1}{a}$)=$\frac{2}{3}$
故答案为:$\frac{2}{3}$.
点评 本题考查了反比例函数的比例系数k的几何意义,解题的关键是正确的用点B的坐标表示出其他点的坐标,从而表示出三角形的面积.

练习册系列答案
相关题目
4.(-0.5)2的平方根是( )
| A. | -0.5 | B. | ±0.5 | C. | 0.5 | D. | 0.25 |
19.甲、乙、丙三人到文具店购买同一种笔记本和钢笔,甲、乙两人购买的数量及总价分别如表:
(1)求笔记本和钢笔的单价;
(2)丙购买24本笔记本和若干支钢笔共花去526元,甲发现丙的总价算错了,请通过计算加以说明.
| 甲 | 乙 | |
| 笔记本(本) | 20 | 15 |
| 钢笔(支) | 12 | 25 |
| 总价(元) | 312 | 330 |
(2)丙购买24本笔记本和若干支钢笔共花去526元,甲发现丙的总价算错了,请通过计算加以说明.
3.下列命题中,不正确的是( )
| A. | 对角线相等的平行四边形是矩形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 三角形的中位线平行于第三边且等于第三边的一半 | |
| D. | 三角形的一条中线能将三角形分成面积相等的两部分 |
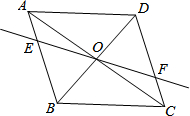 如图,在?ABCD中,对角线AC、BD交于点O,经过点O的直线交AB于E,交CD于F.
如图,在?ABCD中,对角线AC、BD交于点O,经过点O的直线交AB于E,交CD于F.

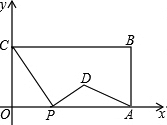 如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=6,OC=4.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.则
如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=6,OC=4.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.则