题目内容
15.已知x,y是实数,且(x-3)2与$\sqrt{2x-y-4}$互为相反数,求实数yx的立方根.分析 根据题意列出关系式,利用非负数的性质得出方程组,求出方程组的解得到x与y的值,即可求出所求的立方根.
解答 解:∵(x-3)2+$\sqrt{2x-y-4}$=0,
∴$\left\{\begin{array}{l}{x-3=0}\\{2x-y-4=0}\end{array}\right.$,
解得:x=3,y=2,
则yx=23=8,8的立方根为2.
点评 此题考查了解二元一次方程组,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
3.等腰三角形顶角是120°,则一腰上的高与另一腰的夹角的度数为( )
| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
2.如果不等式(1+a)x>1+a的解集为x<1,那么a的取值范围是( )
| A. | a>0 | B. | a<0 | C. | a>-1 | D. | a<-1 |
 如图,在平面直角坐标系中xOy中,边长为10的正方形ABCD的对角线AC,BD相交于点P,点A在x轴正半轴上运动,点B在y轴正半轴上运动(正半轴不包含原点O),点C、D都在第一象限.
如图,在平面直角坐标系中xOy中,边长为10的正方形ABCD的对角线AC,BD相交于点P,点A在x轴正半轴上运动,点B在y轴正半轴上运动(正半轴不包含原点O),点C、D都在第一象限.
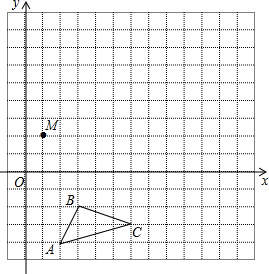 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).
在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).